11+ Maths
Ratios and proportions

Objective: Understand and express the relationship between two or more quantities.
Why Ratio and Proportions Matters: Ratios help compare quantities, while proportions show equality between ratios. These skills are useful in real-life tasks like scaling recipes, mixing solutions, or calculating discounts.
Key Ideas:
A ratio shows how one quantity relates to another.
A proportion shows that two ratios are equal.
11+ Maths
Ratios and proportions
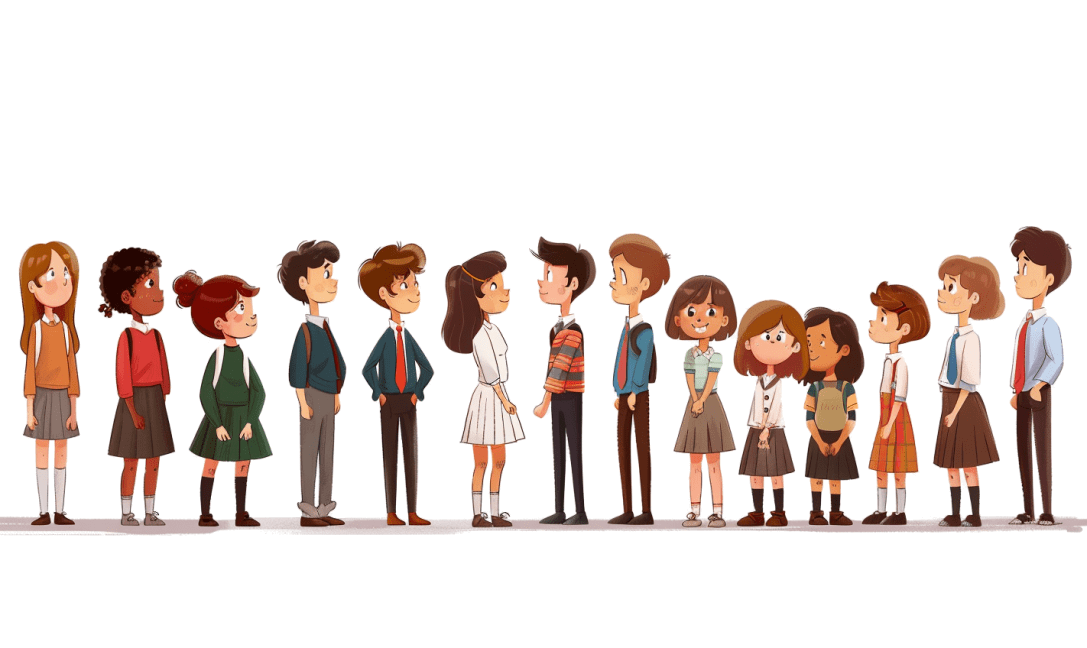
Introduction to Ratios
A ratio is a way to compare two or more quantities to show how much of one thing there is compared to another.
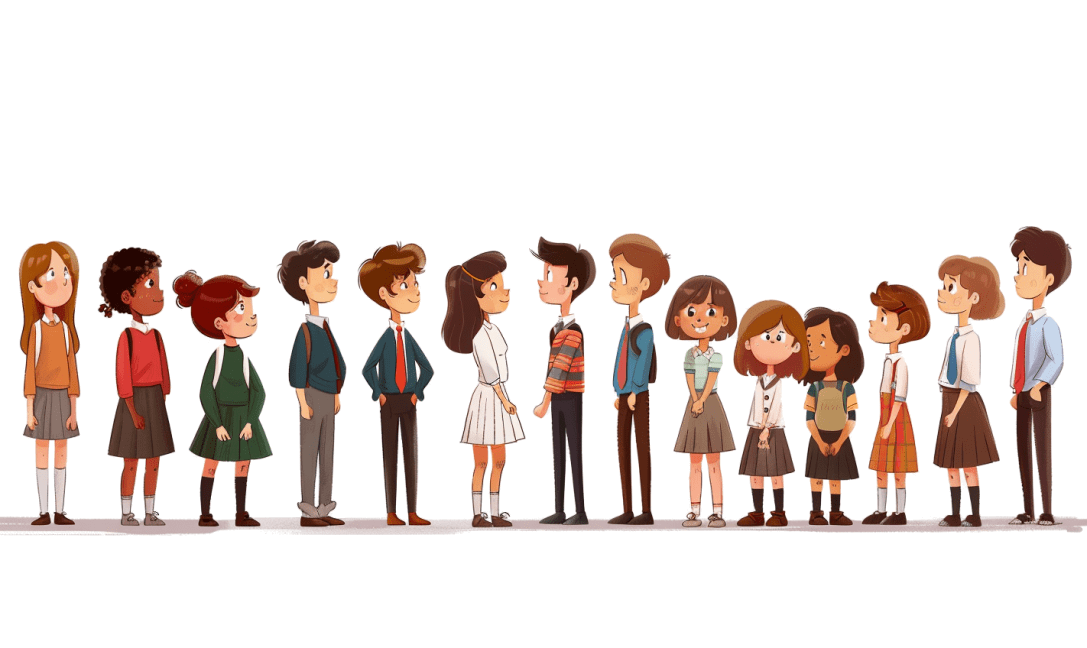
Introduction to Ratios
A ratio is a way to compare two or more quantities to show how much of one thing there is compared to another.
In this class, there are 14 students.
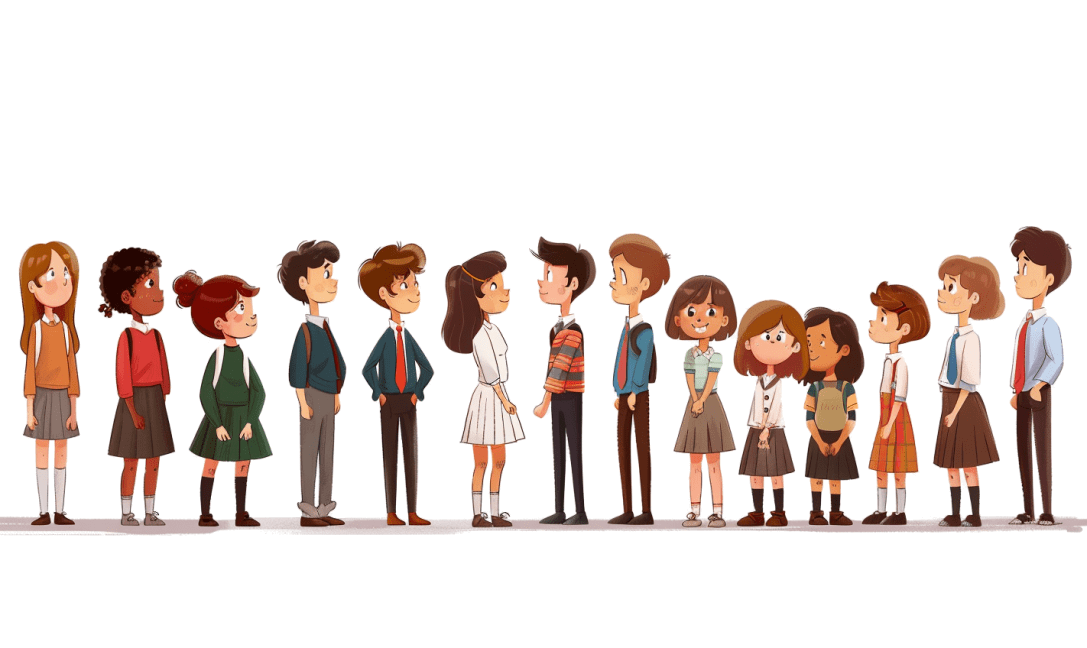
Introduction to Ratios
A ratio is a way to compare two or more quantities to show how much of one thing there is compared to another.
In this class, there are 14 students.
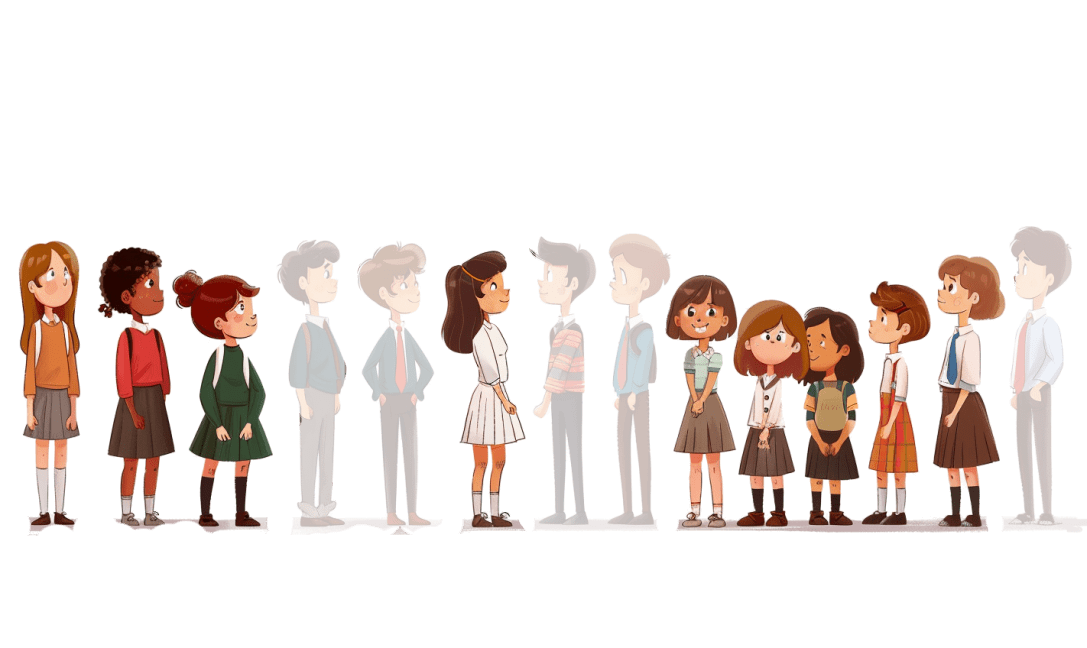
Introduction to Ratios
A ratio is a way to compare two or more quantities to show how much of one thing there is compared to another.
In this class, there are 14 students.
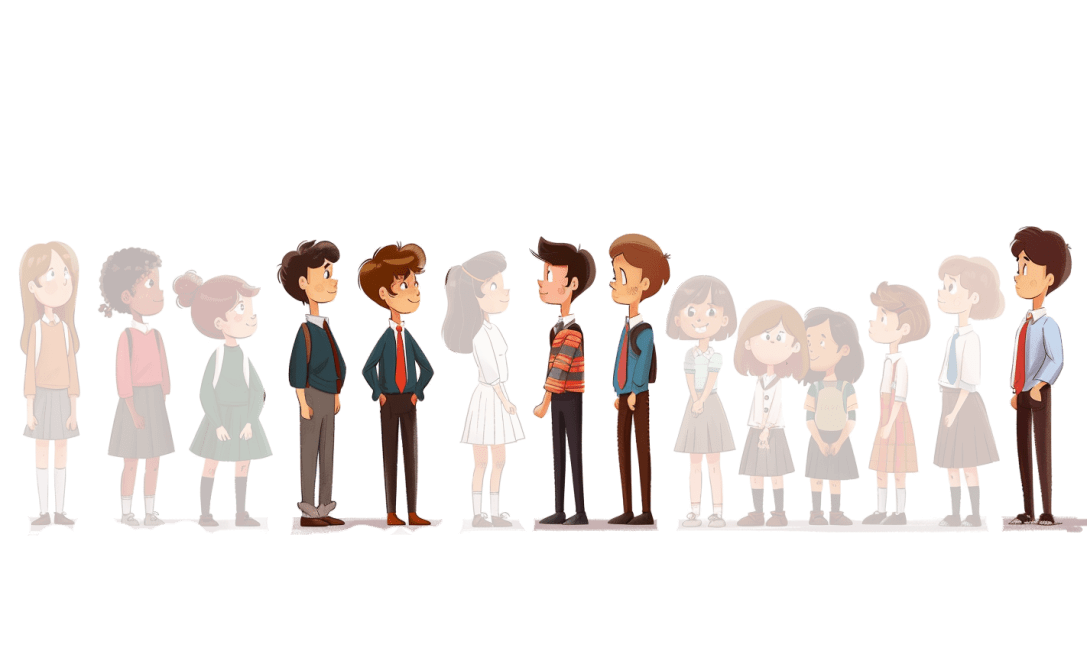
Introduction to Ratios
A ratio is a way to compare two or more quantities to show how much of one thing there is compared to another.
In this class, there are 14 students.

We can express that as a ratio:

We can express that as a ratio:
Since there are 14 students, we can also express the girls and boys as fractions of 14:

We can express that as a ratio:
Since there are 14 students, we can also express the girls and boys as fractions of 14:
9 girls & 5 boys makes the total 14 children
This type of ratio is called part-to-part ratio and is usually express with a colon (:) like here
We express part-to-part ratios by stating the parts, not the whole total. But we can calculate a whole by adding the parts together. In the previous example, we can add the girls and boys together to find the whole class size:
9 girls & 5 boys makes the total 14 children
This type of ratio is called part-to-part ratio and is usually express with a colon (:) like here
We express part-to-part ratios by stating the parts, not the whole total. But we can calculate a whole by adding the parts together. In the previous example, we can add the girls and boys together to find the whole class size:
part-to-part ratio
We express part-to-part ratios by stating the parts, not the whole total. But we can calculate a whole by adding the parts together. In the previous example, we can add the girls and boys together to find the whole class size:
part-to-part ratio
part-to-whole ratio
Another way of expressing this ratio would be as fractions out of the total. We call this part-to-whole ratio:
We express part-to-part ratios by stating the parts, not the whole total. But we can calculate a whole by adding the parts together. In the previous example, we can add the girls and boys together to find the whole class size:
part-to-part ratio
part-to-whole ratio
Another way of expressing this ratio would be as fractions out of the total. We call this part-to-whole ratio:
part-to-whole ratio
Another way of expressing this ratio would be as fractions out of the total. We call this part-to-whole ratio:
In this case, 14 was the actual number of children. But in other cases a ratio may be expressed against a fraction of the actual total. Let's look at some examples:
part-to-whole ratio
Another way of expressing this ratio would be as fractions out of the total. We call this part-to-whole ratio:
In this case, 14 was the actual number of children. But in other cases a ratio may be expressed against a fraction of the actual total. Let's look at some examples:
But, we would express 10 and 20 out of 30 in the same way:
With ratio we're only expressing how parts relate to each other. If there is always twice as many b as a, we'd express it as
It doesn't matter if a=1 and b=2 or a=50 and b=100. The relationship is still 1:2
You will be familiar with this concept from working with fractions in general. You can scale them up or down simply by multiplying both the numerator and the denominator with the same number:
Ratio works in the same way. There is no difference between 1:2 and 5:10. They describe the same ratio.

Let's have a look at some practical examples
We can express this as either
In this case we have one apple and one orange, so the ratio would be 1:1 because there is one apple for every one orange.
If we wanted to use a fraction, they'd both be

Let's have a look at some practical examples
Now there are two apples and two oranges. The ratio is still 1:1 because there is still 1 apple for every 1 orange.

Let's have a look at some practical examples
With three apples and three oranges, the ratio is still 1:1. You could express it as 3:3 but this simplifies to 1:1. We are simply saying that there are still 1 apple for ever 1 orange.

Let's have a look at some practical examples
Now the ratio is no longer 1:1. There is not 1 apple for every 1 orange.
The ratio is now 4:3. There are 4 apples for every 3 oranges. As fractions we would say:

Let's have a look at some practical examples
Now the ratio is no longer 1:1. There is not 1 apple for every 1 orange.
The ratio is now 4:3. There are 4 apples for every 3 oranges. As fractions we would say:
Simplifying Ratios

Ratio =
As we mentioned earlier, ratio can be simplified, the same way as fractions. To simplify a ratio, divide all parts of the ratio by their greatest common factor (GCF). Always simplify ratios to their smallest whole numbers.
Example:
The GCF (6 and 9) = 3
Simplifying Ratios
As we mentioned earlier, ratio can be simplified, the same way as fractions. To simplify a ratio, divide all parts of the ratio by their greatest common factor (GCF). Always simplify ratios to their smallest whole numbers.

Ratio =
If you look closer, you can actually visualise how 3 oranges go with every 2 pears.
Proportions
As we have seen, ratios tell us how much of one thing there is in relation to another thing: "For every 2 apples we have 3 bananas" (2:3)
Proportions tell us about how much of one thing there is in relation to the whole amount of something. For example:
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
How many apples are there?
Proportions
"
How many apples are there?
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
1
5
25
Proportions
"
How many apples are there?
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
1
5
25
Proportions
"
How many apples are there?
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
1
5
25
Proportions
"
How many apples are there?
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
1
5
25
Proportions
"
How many apples are there?
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
1
5
25
Proportions
"
How many apples are there?
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
1
5
25
Proportions
"
How many apples are there?
There are 25 pieces of fruit, and 1 in every 5 of those is an apple.
25
Another example of proportions
- Example: If 4 oranges cost £2, how much will 10 oranges cost at the same rate?
Answer: The proportion can be set up as:
Where:
-
444 is the number of oranges,
-
222 is the cost for 4 oranges,
-
101010 is the number of oranges for which we need to find the cost,
-
xxx is the unknown cost of 10 oranges.
4 oranges cost £2
10 oranges cost £x
- Example: If 4 oranges cost £2, how much will 10 oranges cost at the same rate?
Answer: The proportion can be set up as:
Where:
-
444 is the number of oranges,
-
222 is the cost for 4 oranges,
-
101010 is the number of oranges for which we need to find the cost,
-
xxx is the unknown cost of 10 oranges.
Another example of proportions
- Example: If 4 oranges cost £2, how much will 10 oranges cost at the same rate?
Answer: Using the cross-multiplication method we get:
By dividing the both sides of the equation by 4 we get:
We get that the price for 10 oranges is £5.
Another example of proportions
Application of Ratio and Proportions
Real-World Examples:
- Recipe Scaling: If a recipe calls for 2 cups of flour for 4 servings, how much flour is needed for 10 servings?
- Map Reading: If 1 cm on a map equals 100 km, how many kilometres does 5 cm represent?
- Medication Dosages: A doctor prescribes 10 mg of medicine per 5 kg of body weight. How much medicine should a 70 kg patient take?
- Population Ratios: In a city of 100,000 people, 60% are adults. How many adults live in the city?
1100=3x\frac{1}{100} = \fr
Application of Ratio and Proportions
Real-World Examples:
- Recipe Scaling: If a recipe calls for 2 cups of flour for 4 servings, how much flour is needed for 10 servings?
- Map Reading: If 1 cm on a map equals 100 km, how many kilometres does 5 cm represent?
- Medication Dosages: A doctor prescribes 10 mg of medicine per 5 kg of body weight. How much medicine should a 70 kg patient take?
- Population Ratios: In a city of 100,000 people, 60% are adults. How many adults live in the city?
1100=3x\frac{1}{100} = \fr
Before we review the solution, try working through these problems step-by-step. You'll be surprised how simple it is!
Application of Ratio and Proportions
Real-World Examples:
1. Recipe Scaling: If a recipe calls for 3 cups of flour for 6 servings, how much flour is needed for 10 servings?
Answer: We need 5 cups of flour for 10 servings.
2. Map Reading: If 1 cm on a map equals 100 km, how many kilometres does 5 cm represent?
1100=3x\frac{1}{100} = \fr
Answer: 5cm on the map represents 500km in real life.
Application of Ratio and Proportions
Real-World Examples:
3. Medication Dosages: A doctor prescribes 10 mg of medicine per 5 kg of body weight. How much medicine should a 70 kg patient take?
4. Population Ratios: In a city of 100,000 people, 60% are adults. How many adults live in the city?
1100=3x\frac{1}{100} = \fr
Answer: In the city live 60,000 adults.
Answer: 70kg person should take 140mg of medicine.
If you compare the two areas and you may notice that we doubled each side, but the area increased 4 times.
This is because the area is the product of the two sides, so the increase of the area will be equal to: increase length x increase width
Thus, if you made each side 10 times longer, the area would increase by 100 times (10 x 10).
This is important to remember if you are converting from e.g. cm to m:

Well done! You should now have a very good understanding of ratios and proportions. You know how to read the ratios, manipulate them by scaling up and down and how to apply this to real problems.
With this information you should be one step closer to nailing the 11+ assessment. Good luck!
11+ Maths :: Ratio and Proportions
By Pluspapers
11+ Maths :: Ratio and Proportions
- 90



