11+ Maths
Number sequences


Objective: Understand patterns in number sequences and learn how to predict future terms.
What We'll Learn: Recognizing different types of sequences (e.g., linear, geometric). Finding rules or formulas for sequences and Solving problems using sequence patterns.
Why it's important: Understanding number sequences helps develop logical thinking and problem-solving skills. These skills are essential in maths and real-life situations like spotting trends or solving puzzles.

11+ Maths
Number sequences
Linear number sequences
A linear sequence is a list of numbers where each term increases or decreases by the same amount (called the common difference).
a1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Let's take this sequence:
The common difference would be the difference between
and
or
and
and so on.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Let's look at some practical examples.
a1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Linear number sequences
A linear sequence is a list of numbers where each term increases or decreases by the same amount (called the common difference).
a1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Let's take this sequence:
The common difference would be the difference between
and
or
and
and so on.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Let's look at some practical examples.
a1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Linear number sequences
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Let's look at some practical examples.
a1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
It's easy to see that the common difference here is +5. In other words, for each step, the number increases by 5. The next number in the sequence would be 40.
Linear number sequences
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
It's easy to see that the common difference here is +5. In other words, for each step, the number increases by 5. The next number in the sequence would be 40.
But what would the 128th number in the sequence be?
Linear number sequences
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
It's easy to see that the common difference here is +5. In other words, for each step, the number increases by 5. The next number in the sequence would be 40.
But what would the 128th number in the sequence be?
Rather than counting on, we can try to write a formula that expresses the number sequence:
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Rather than counting on, we can try to write a formula that expresses the number sequence:
We know that the size of the number increases with 5 each time we step forward. If we call the number of steps , we could express it this way:
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Rather than counting on, we can try to write a formula that expresses the number sequence:
We know that the size of the number increases with 5 each time we step forward. If we call the number of steps , we could express it this way:
But this isn't quite right. If we test this, we see that the first number in the sequence should be 5 x 1=5 and the
second 5 x 2 = 10 etc. What we are missing is the starting value.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
But this isn't quite right. If we test this, we see that the first number in the sequence should be 5 x 1=5 and the
second 5 x 2 = 10 etc. What we are missing is the starting value. By adding , we correct for this.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?

Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?

Worded problems
We can use our understanding of number sequences to efficiently solve worded problems.
Let's use number sequences to solve this worded problem:
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
First we need to establish whether this is a linear number sequence. To do so we need to ask ourselves: Does the relevant numbers increase by a set amount for each step?
In this case the answer is YES. The amount goes up by the same amount every day.
increase by a set amount for each step?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
increase by a set amount for each step?
1. Does the number
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
increase by a set amount for each step?
1. Does the number
Now, we need to find the formula for the increase. In this case the amount goes up by £5 each day.
We can write this as "5n". This is shorthand for 5 x n: for every time we take one step on the timeline, the amount goes up 5. So, for two days the amount will be two times five = 10, for 3 days it will be three times five and so on.
the formula for the increase.
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
increase by a set amount for each step?
1. Does the number
2. Find
the formula for the increase.
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
increase by a set amount for each step?
1. Does the number
2. Find
the formula for the increase.
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Finally, we need to identify the starting amount. In this case, the text says that Anna started with £20 on the account - we therefore need to add that amount to the formula. This is a fixed amount that is not dependant on the number of steps, so we can write this as +£20.
the starting amount
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
increase by a set amount for each step?
1. Does the number
2. Find
3. Identify
the formula for the increase.
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
the starting amount.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
increase by a set amount for each step?
1. Does the number
2. Find
3. Identify
the formula for the increase.
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
the starting amount.
Let's put it all together to find the correct linear formula for this worded problem.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
1. Does the number increase by a set amount for each step?
2. Find the formula for the increase.
3. Identify the starting amount.
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Yes.
5n
+20
5n
+20
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
1. Does the number increase by a set amount for each step?
2. Find the formula for the increase.
3. Identify the starting amount.
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
Yes.
5n
+20
5n
+20
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
We have now "translated" the events into a maths formula:
5n
+20
5n
+20
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
We have now "translated" the events into a maths formula:
5n
+20
5n
+20
We start with a fixed amount of 20, and for each step we add 5 more.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
5n
+20
5n
+20
We start with a fixed amount of 20, and for each step we add 5 more.
We're now ready to answer the question: "How much does Anna have at the end of the 20 day period?"
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
5n
+20
5n
+20
We're now ready to answer the question: "How much does Anna have at the end of the 20 day period?"
The letter "n" represents the number of steps - in this case days. So, let's replace n with 20.
20
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
5x20
+20
5n
+20
We're now ready to answer the question: "How much does Anna have at the end of the 20 day period?"
The letter "n" represents the number of steps - in this case days. So, let's replace n with 20.
20
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
5x20
+20
5n
+20
We're now ready to answer the question: "How much does Anna have at the end of the 20 day period?"
Now, all we need to do is to follow normal BODMAS rules to find the total.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
100
+20
5n
+20
We're now ready to answer the question: "How much does Anna have at the end of the 20 day period?"
Now, all we need to do is to follow normal BODMAS rules to find the total.
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
120
5n
+20
We're now ready to answer the question: "How much does Anna have at the end of the 20 day period?"
£
Leta1,a2,a3,a4,…a_1, a_2, a_3, a_4, \dots
an=a1+(n−1)⋅da_n = a_1 + (n - 1) \cdot d
Now we can verify that our formula makes sense:
1st term:
2nd term:
3rd term:
With this formula we can also quickly answer the original question: What is the 128th term in this sequence?
Anna has £20 in her savings account. Now she wants to save more. She decides to deposit £5 into her savings account each day for 20 days. How much does Anna have at the end of the 20 day period?
"
"
120
5n
+20
We're now ready to answer the question: "How much does Anna have at the end of the 20 day period?"
£
Let's try another sequential problem

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
Let's try another sequential problem

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
Let's try another sequential problem

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this.
Let's try another sequential problem

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?
Yes. Apart from the first pyramid, the number required to make each new pyramid is the same.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?
Yes. Apart from the first pyramid, the number required to make each new pyramid is the same.
2. Find the formula for the increase.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?
Yes. Apart from the first pyramid, the number required to make each new pyramid is the same.
2. Find the formula for the increase.
Since the increase is two lines each time, the formula for the increase is 2n.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?
Yes. Apart from the first pyramid, the number required to make each new pyramid is the same.
2. Find the formula for the increase.
Since the increase is two lines each time, the formula for the increase is 2n.
3. Identify the starting amount.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?
Yes. Apart from the first pyramid, the number required to make each new pyramid is the same.
2. Find the formula for the increase.
Since the increase is two lines each time, the formula for the increase is 2n.
3. Identify the starting amount.
If we look closely, we can see that 3 lines were required for the first pyramid. That is one more than for all the others. So, we can think of our starting amount as +1.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?
Yes. Apart from the first pyramid, the number required to make each new pyramid is the same.
2. Find the formula for the increase.
Since the increase is two lines each time, the formula for the increase is 2n.
3. Identify the starting amount.
If we look closely, we can see that 3 lines were required for the first pyramid. That is one more than for all the others. So, we can think of our starting amount as +1.
2n
+1

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Let's solve this by using a linear sequential formula:
1. Does the number of lines increase by a set amount for each step?
Yes. Apart from the first pyramid, the number required to make each new pyramid is the same.
2. Find the formula for the increase.
Since the increase is two lines each time, the formula for the increase is 2n.
3. Identify the starting amount.
If we look closely, we can see that 3 lines were required for the first pyramid. That is one more than for all the others. So, we can think of our starting amount as +1.
2n
+1

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
Let's solve this by using a linear sequential formula:
2n
+1
Now that we have the formula, we can plug in the numbers from the question.
50
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
Let's solve this by using a linear sequential formula:
2x50
+1
Now that we have the formula, we can plug in the numbers from the question.
50
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Finally, we can calculate the answer.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
Let's solve this by using a linear sequential formula:
100
+1
Now that we have the formula, we can plug in the numbers from the question.
50
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Finally, we can calculate the answer.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
Let's solve this by using a linear sequential formula:
101
+1
Now that we have the formula, we can plug in the numbers from the question.
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
Finally, we can calculate the answer.

Addi Shun is playing with pyramid shapes in the sand. First he draws a simple pyramid:
He realises that if he turns every second pyramid upside-down, he can stack them together like this:
Let's solve this by using a linear sequential formula:
It required 7 lines to make three pyramids. How many lines must he draw to make 50 pyramids?
101
+1

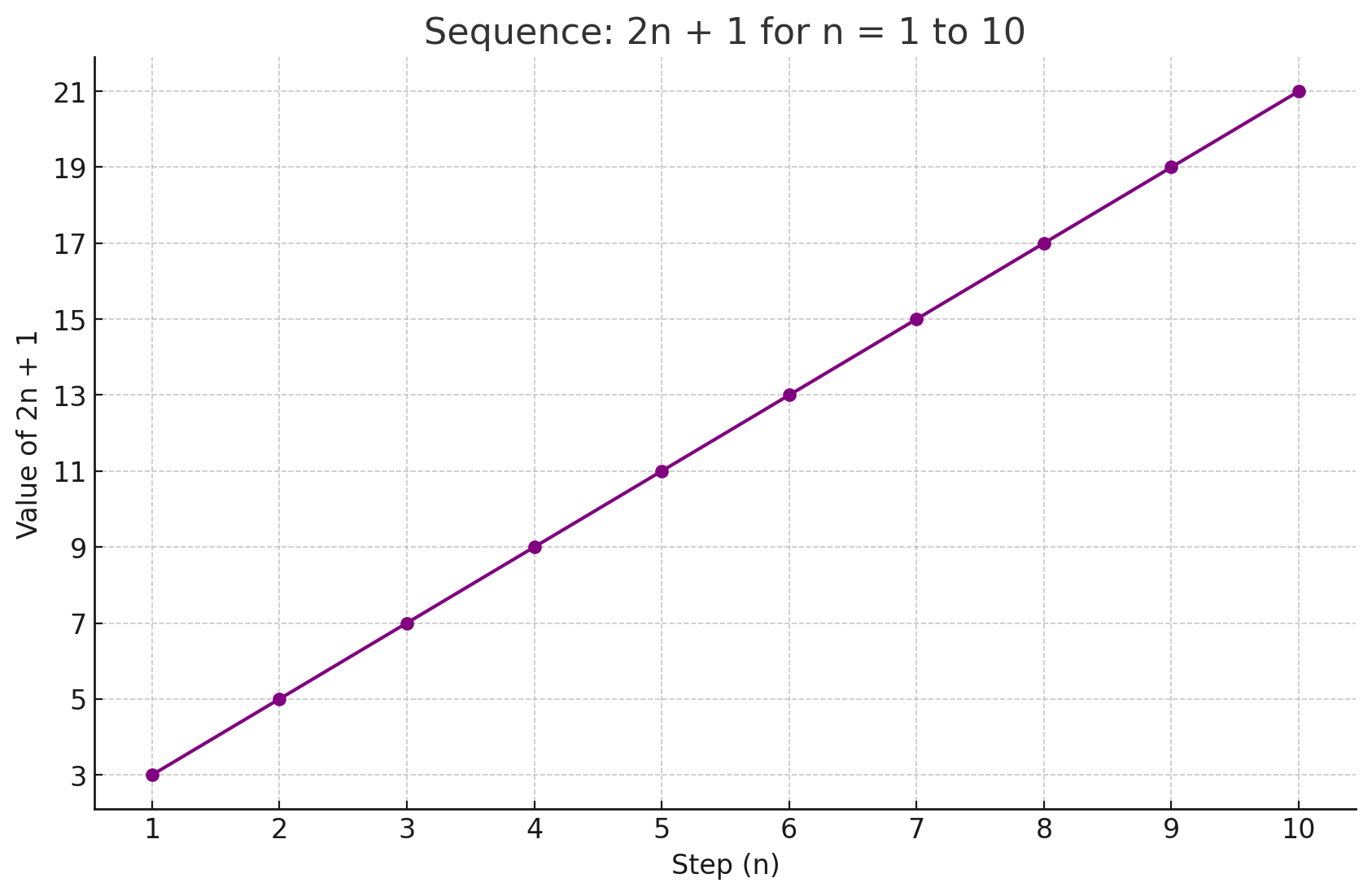
So far we have looked at sequences with linear growth. These are sequences where the value increases by the same amount each step. As we saw, the equation 2n + 1 makes the value go up by 2 each step.
If you were to draw these values as a graph, they'd look like a straight line.
If you were to draw these values as a graph, they'd look like a straight line.

If you were to draw these values as a graph, they'd look like a straight line.

If you were to draw these values as a graph, they'd look like a straight line.
But a sequence doesn't have to be linear. Have a look at the sequence below.
If you were to draw these values as a graph, they'd look like a straight line.
But a sequence doesn't have to be linear. Have a look at the sequence below.
It's easy to recognise this as a doubling sequence. For each step we simply double the value.
If you were to draw these values as a graph, they'd look like a straight line.
But a sequence doesn't have to be linear. Have a look at the sequence below.
It's easy to recognise this as a doubling sequence. For each step we simply double the value.
The increase is logical, but it is not linear. The increase each time is not the same. Therefore, we cannot use times to express this; as you may recall, if we used 2n, we were simply adding two each time. But while this works from 2 to 4, it does not work from 4 to 8 or from 8 to 16 etc.
+2
+4
+8
+16
+32
+64
128
If you were to draw these values as a graph, they'd look like a straight line.
But a sequence doesn't have to be linear. Have a look at the sequence below.
+2
+4
+8
+16
+32
+64
128
Let's organise the figures in a table.
If you were to draw these values as a graph, they'd look like a straight line.
But a sequence doesn't have to be linear. Have a look at the sequence below.
+2
+4
+8
+16
+32
+64
128
Let's organise the figures in a table.
If you were to draw these values as a graph, they'd look like a straight line.
But a sequence doesn't have to be linear. Have a look at the sequence below.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
If you were to draw these values as a graph, they'd look like a straight line.
But a sequence doesn't have to be linear. Have a look at the sequence below.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
It works for all the numbers in the series (and beyond):
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
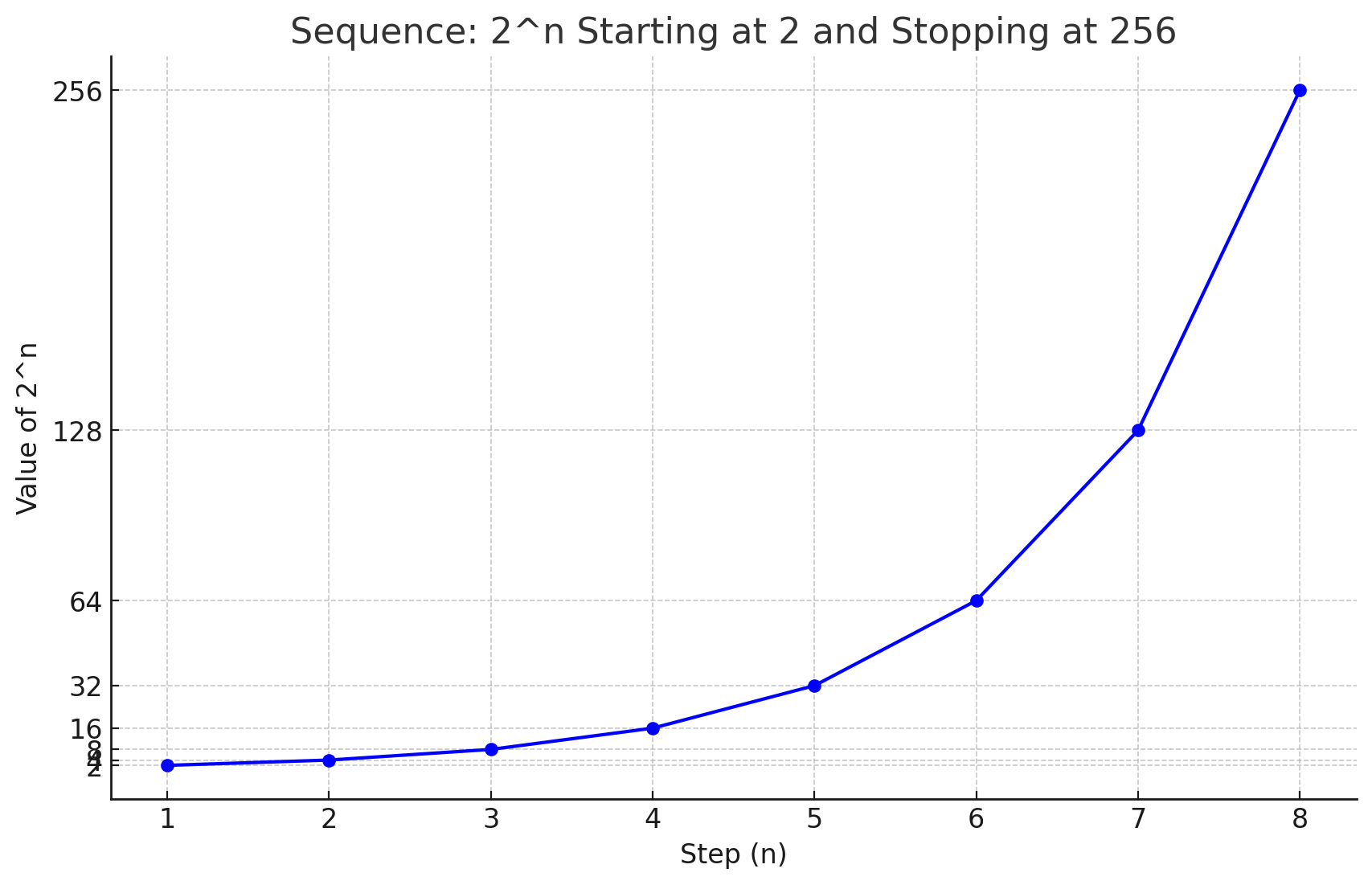
If we plot the values, we can see that this is not a linear graph. Because we are doubling the previous value, each step gets bigger and bigger.
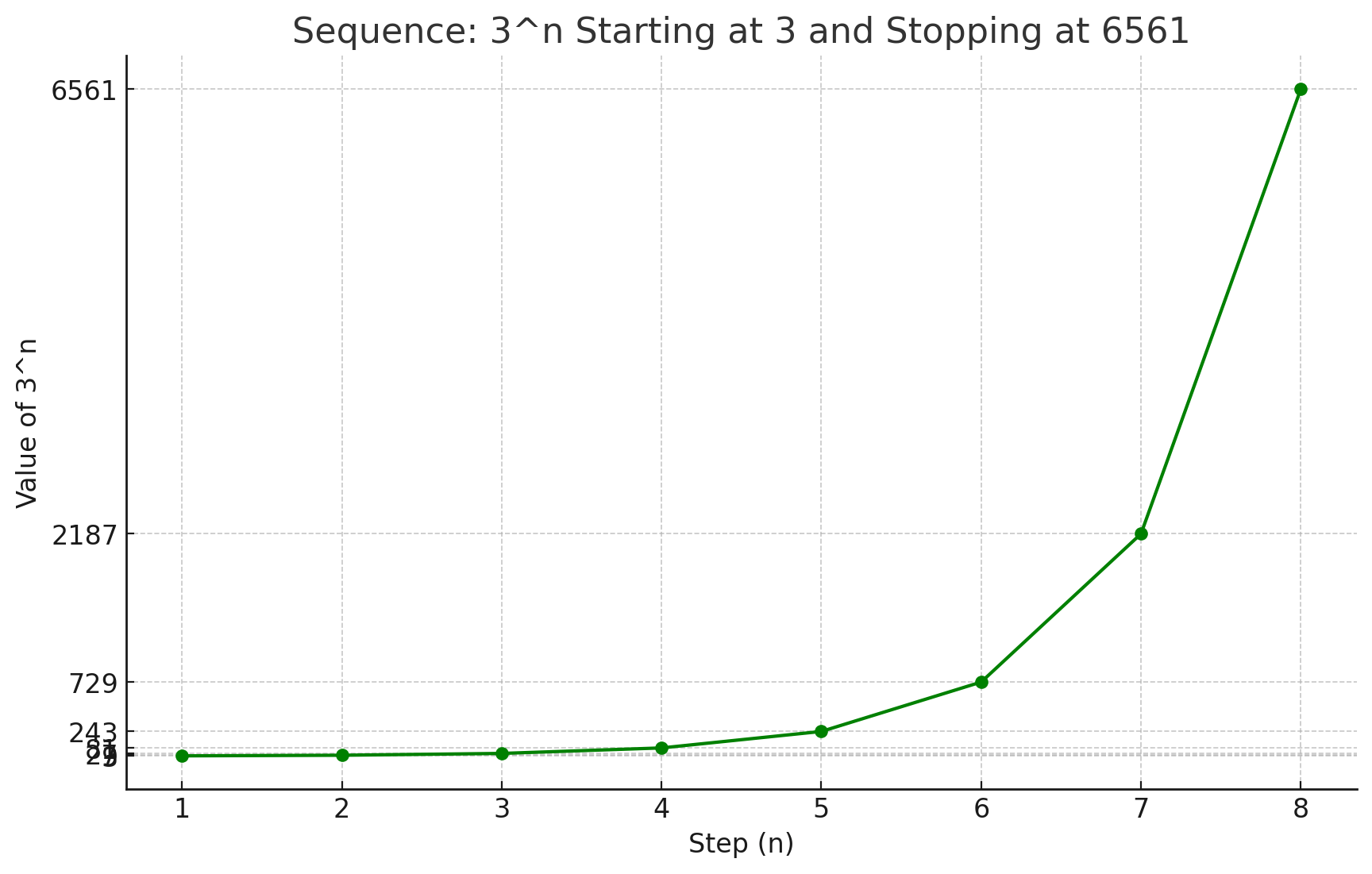
If we change the 2 to a 3, we'd be tripling the value. This is because we'd have 3, 3x3, 3x3x3, 3x3x3x3 and so on. As you can see the formula means we add a x3 (triple) each step.
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If we plot the values, we can see that this is not a linear graph. Because we are doubling the previous value, each step gets bigger and bigger.
If we change the 2 to a 3, we'd be tripling the value. This is because we'd have 3, 3x3, 3x3x3, 3x3x3x3 and so on. As you can see the formula means we add a x3 (triple) each step.
If you were to draw these values as a graph, they'd look like a straight line.
+2
+4
+8
+16
+32
+64
128
So if n (the "step") is 1, then the sum is 2, if n is 2, then the value is 4, if n is 3 the value is 8 and so on.
We can express this as
If we plot the values, we can see that this is not a linear graph. Because we are doubling the previous value, each step gets bigger and bigger.
This type of growth, where each jump gets bigger and bigger is sometimes referred to as exponential growth as opposed to the linear growth we explored earlier (e.g. )

Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
The Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers:
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
The Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers:
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
The Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers:
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
The Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers:
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
The Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers:
Fibonacci sequence
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
The Fibonacci sequence is a sequence of numbers where each number is the sum of the two preceding numbers:
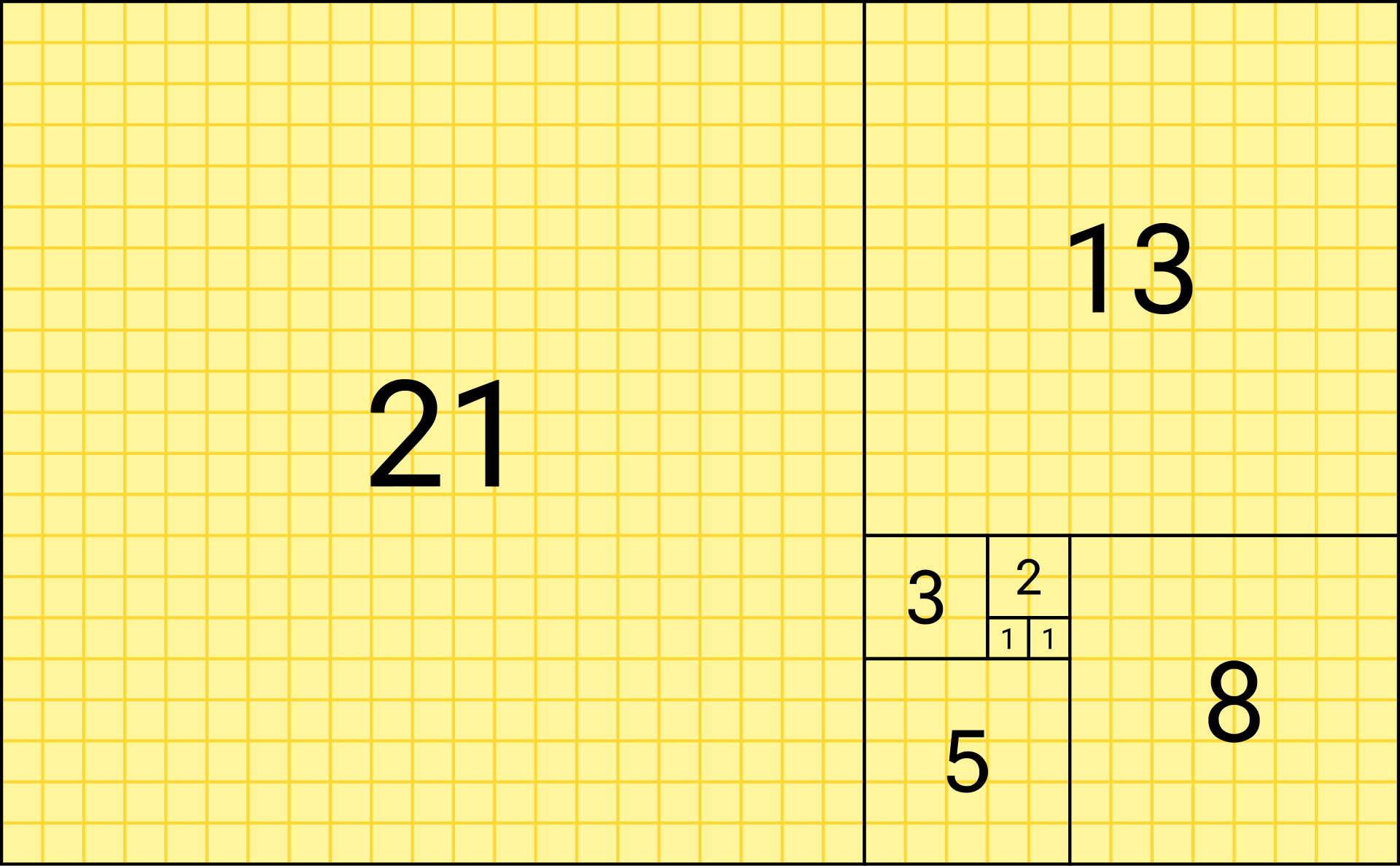
The Fibonacci sequence is often expressed graphically like this; or sometimes with a spiral shape.
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
Prime number sequences are, as the name implies, sequences of prime numbers:
prime number sequences
Since there is no simple system to prime numbers, we cannot easily express a prime number sequence as a function of n. The important thing is that you can identify these sequences as sequences of prime numbers.
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
prime number sequences
Since there is no simple system to prime numbers, we cannot easily express a prime number sequence as a function of n. The important thing is that you can identify these sequences as sequences of prime numbers.

Well done! You should now have a good understanding of number sequences, how to interpret them, how to make them into mathematical formulae and how you can use them to solve more complex questions.
With this information you should be one step closer to nailing the 11+ assessment. Good luck!
11+ Maths :: Number sequences
By Pluspapers
11+ Maths :: Number sequences
- 67



