Number and Place Value

Number and Place Value
- Place value
- Comparing large numbers
- Rounding numbers
- Negative numbers
- Factors and multiples
- Highest common factor (HCF) and lowest common factor (LCM)
- Prime numbers
- Square and cube numbers

Place value

Place value
Place Value
Place Value
Place value is a way of understanding how much each digit in a number is worth, based on where it is in the number.
Each place in a number has a specific role. We use a decimal system, which means that the value of each number increases 10 times for each place:
Place Value
Place value is a way of understanding how much each digit in a number is worth, based on where it is in the number.
Each place in a number has a specific role. We use a decimal system, which means that the value of each number increases 10 times for each place:
Place Value
Place value is a way of understanding how much each digit in a number is worth, based on where it is in the number.
Each place in a number has a specific role. We use a decimal system, which means that the value of each number increases 10 times for each place:
Place Value
Place value is a way of understanding how much each digit in a number is worth, based on where it is in the number.
Each place in a number has a specific role. We use a decimal system, which means that the value of each number increases 10 times for each place:
Place Value
Place value is a way of understanding how much each digit in a number is worth, based on where it is in the number.
Each place in a number has a specific role. We use a decimal system, which means that the value of each number increases 10 times for each place:
This number now means 10
and this number means 1
So the total value is 10+1
Place Value
Place value is a way of understanding how much each digit in a number is worth, based on where it is in the number.
Each place in a number has a specific role. We use a decimal system, which means that the value of each number increases 10 times for each place:
This number is just a simple way of writing
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
This row represents the 1s. There can be a one or there can be zero ones.
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Because this is a binary system, the this row represents not the 10s but the 2s
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
And this row represents the 2 x 2, so we can say it represents the 4s
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
Finally, this number represents the 2 x 2 x 2 = 8s.
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
There are number systems that are not base-10:
Computers are built on a binary system (base-2)
This number is made up of:
Place Value
We call the maximum value of each number column a "base value". Because we use a decimal system, our number system is a base-10 system.
Computers are built on a binary system (base-2)
There are other base systems too, such as base-16.
The Babylonians used a base-60 systems!
And the Roman's didn't use a real base system at all. In Roman numerals the row doesn't have a specific meaning. Instead each number has a symbol.
Place Value
And the Roman's didn't use a real base system at all. In Roman numerals the row doesn't have a specific meaning. Instead each number has a symbol.
2026 is MMXXVI in Roman numerals
The symbol M = 1000. There's two of them, so 2 x 1000 = 2000
The symbol X means 10. Again, there are two of them, so 2 x 10 = 20
V means 5. There's one of these, so 1 x 5 = 5
Place Value
And the Roman's didn't use a real base system at all. In Roman numerals the row doesn't have a specific meaning. Instead each number has a symbol.
2026 is MMXXVI in Roman numerals
The symbol M = 1000. There's two of them, so 2 x 1000 = 2000
The symbol X means 10. Again, there are two of them, so 2 x 10 = 20
V means 5. There's one of these, so 1 x 5 = 5
I means 1. There's one I, so we have 1 x 1 = 1
2000
20
5
1
Place Value
And the Roman's didn't use a real base system at all. In Roman numerals the row doesn't have a specific meaning. Instead each number has a symbol.
2026 is MMXXVI in Roman numerals
The symbol M = 1000. There's two of them, so 2 x 1000 = 2000
The symbol X means 10. Again, there are two of them, so 2 x 10 = 20
V means 5. There's one of these, so 1 x 5 = 5
I means 1. There's one I, so we have 1 x 1 = 1
2000
20
5
1
2026
Place Value
In our own decimal system, however, the position of a number determines it's value. Let's analyse a larger number:
4 2 0 5 3 1 7
Place Value
In our own decimal system, however, the position of a number determines it's value. Let's analyse a larger number:
4 2 0 5 3 1 7
7 is in the ones place, so it's worth 7
1 is in the tens place, so it's worth 10
3 is in the hundreds place, so it's worth 300
5 is in the thousands place, so it's worth 5000
0 is in the ten thousands place - it's worth 0 (it holds the place for that value!)
2 is in the hundred thousands place so it's worth 200,000
4 is in the millions place, so it's worth 4,000,000
4
2
0
5
3
1
7
Place Value
In our own decimal system, however, the position of a number determines it's value. Let's analyse a larger number:
4 2 0 5 3 1 7
4
2
0
5
3
1
7
Place Value
Understanding place value helps you with everything in maths - reading, writing, rounding and even multiplying big numbers!
Practice: For each digit in the number 8,506, write its value.
8,506
6
0
500
8000
Ordering and Comparing Numbers
Ordering numbers means arranging numbers either from smallest to biggest (ascending order) or biggest to smallest (descending order).
Ordering and Comparing Numbers
Ordering numbers means arranging numbers either from smallest to biggest (ascending order) or biggest to smallest (descending order).
Let's organise these numbers in descending order
Ordering and Comparing Numbers
Let's organise these numbers in descending order
Ordering and Comparing Numbers
Let's organise these numbers in descending order
Let's start by sorting by the left-most digits (the largest value) first.
Ordering and Comparing Numbers
Let's organise these numbers in descending order
Now, let's sort by the next digit too. As you can see they are already in the right order: 20, 20, 18, 12 and 12
Let's start by sorting by the left-most digits (the largest value) first.
Ordering and Comparing Numbers
Now, let's sort by the next digit too. As you can see they are already in the right order: 20, 20, 18, 12 and 12
Let's start by sorting by the left-most digits (the largest value) first.
Now, include the three first digits from the left. The order is still correct: 202, 201, 184, 125 and 125.
Ordering and Comparing Numbers
Now, let's sort by the next digit too. As you can see they are already in the right order: 20, 20, 18, 12 and 12
Now, include the three first digits from the left. The order is still correct: 202, 201, 184, 125 and 125.
We can now compare by the last digit. As you see, the two last two numbers must switch place.
Ordering and Comparing Numbers
That's it. We have sorted the numbers in descending order.
Ordering and Comparing Numbers
Comparing numbers helps us find out if one number is equal to, smaller than or bigger than another number.
Symbols to know:
Equal to = means both numbers are the same.
Example: 5 = 5
Greater than > means the first number is bigger
Example: 8 > 3
Less than < means the first number is smaller
Example: 2 < 7
Ordering and Comparing Numbers
Practice: Compare these numbers using <, >, =
342 456
1230 1230
9876 7654
4321678 4329876
<
=
>
<
Ordering and Comparing Numbers
Practice: Compare these numbers using <, >, =
342 456
1230 1230
9876 7654
4321678 4329876
<
=
>
<
Again we use the method of scanning left to right
Ordering and Comparing Numbers
Practice: Compare these numbers using <, >, =
342 456
1230 1230
9876 7654
4321678 4329876
<
=
>
<
Again we use the method of scanning left to right
Ordering and Comparing Numbers
Practice: Compare these numbers using <, >, =
342 456
1230 1230
9876 7654
4321678 4329876
<
=
>
<
Again we use the method of scanning left to right
Ordering and Comparing Numbers
Practice: Compare these numbers using <, >, =
342 456
1230 1230
9876 7654
4321678 4329876
<
=
>
<
Again we use the method of scanning left to right
Ordering and Comparing Numbers
Practice: Compare these numbers using <, >, =
342 456
1230 1230
9876 7654
4321678 4329876
<
=
>
<
Again we use the method of scanning left to right
From the fourth digit, we can conclude that the number on the right is the largest.
Rounding Numbers
Rounding makes a number simpler while keeping its value close to the original.
It can help us estimate quantities quickly and it can be a good way of double checking answers.
To round a decimal to a given place:
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
Rounding Numbers
Example: Round 763 to the nearest ten.
As we are rounding to tens, we look first at the units (to the right of the tens)
The value is 3, which is less than 5
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
Rounding Numbers
Example: Round 763 to the nearest ten.
As we are rounding to tens, we look first at the units (to the right of the tens)
The value is 3, which is less than 5
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
We keep the value 6 and we change the following values to 0
Rounding Numbers
Example: Round 763 to the nearest ten.
As we are rounding to tens, we look first at the units (to the right of the tens)
The value is 3, which is less than 5
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
We keep the value 6 and we change the following values to 0
Rounding Decimals
Let's try one more, step-by-step
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
Round to nearest thousandth
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
First, identify the thousands place
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
Look at the value to the right.
It's more than 5.
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
We change the thousands up one from 7 to 8
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
We set all the following values to 0
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
- Set the preceding values to 0
Negative Numbers
Negative Numbers
Negative numbers are numbers that are less than 0. They are written with a minus sign in front.
Examples: -3, -7, -15.
Where do we use negative numbers?
-
Temperature: -5°C is colder than 0°C
-
Money: If you owe £10, it's written as -£10
-
Depth: Below sea level is negative, around -50 metres
Negative Numbers
How to compare negative numbers:
0
1
2
3
4
-4
-3
-2
-1
Numbers increasing
Numbers decreasing
On a number line, numbers increase as you move right and decrease as you move left. The more negative a number is, the smaller it is.
Negative Numbers
Practice: Find the largest number from the following list.
-1342 -1508 -1511 -1430
Final answer: The largest number is -1342.
Remember the more negative a number is, the smaller it is. Closer to zero → larger value.
-
-1342 is closest to zero.
-
-1430 is the next closest.
-
-1508 is further from zero.
-
-1511 is the farthest from zero (smallest value)
Negative Numbers
Adding negative numbers
Because negative numbers represent less than 0, when you add them to a positive number, they will make the total lower, not higher.
Negative Numbers
Adding negative numbers
Because negative numbers represent less than 0, when you add them to a positive number, they will make the total lower, not higher.
Negative Numbers
Adding negative numbers
Because negative numbers represent less than 0, when you add them to a positive number, they will make the total lower, not higher.
Negative Numbers
Adding negative numbers
Because negative numbers represent less than 0, when you add them to a positive number, they will make the total lower, not higher.
You can imagine this on a number line where positive numbers increase to the right and negative numbers to the left:
Negative Numbers
Adding negative numbers
Because negative numbers represent less than 0, when you add them to a positive number, they will make the total lower, not higher.
You can imagine this on a number line where positive numbers increase to the right and negative numbers to the left:
The -3 represents three jumps to the left.
Negative Numbers
Adding negative numbers
Because negative numbers represent less than 0, when you add them to a positive number, they will make the total lower, not higher.
You can imagine this on a number line where positive numbers increase to the right and negative numbers to the left:
The -3 represents three jumps to the left.
The +5 represents five jumps to the right.
Factors and Multiples
Factors and Multiples
12
1 x 12
2 x 6
3 x 4
Example:
A factor of a number is a number that divides into it exactly, without leaving a remainder.
Factors and Multiples
12
1 x 12
2 x 6
3 x 4
Example:
The factors of 12 are 1, 2, 3, 4, 6 and 12.
1
12
2
6
3
4
A factor of a number is a number that divides into it exactly, without leaving a remainder.
Factors and Multiples
A factor of a number is a number that divides into it exactly, without leaving a remainder.
12
1 x 12
2 x 6
3 x 4
Example:
The factors of 12 are 1, 2, 3, 4, 6 and 12.
1
12
2
6
3
4
The highest common factor (HCF) is the largest factor that two or more numbers have in common.
Example: Find the HCF of 12 and 16.
Factors of 12: 1, 2, 3, 4, 6, 12.
Factors of 18: 1, 2, 3, 6, 9, 18.
Which factors do 12 and 18 have in common?
1, 2, 3, 6 are common factors.
Factors and Multiples
The largest common factor is 6
The highest common factor (HCF) is the largest factor that two or more numbers have in common.
Factors and Multiples
HCF are important because we can use them to simplify and compare fractions.
Factors and Multiples
HCF are important because we can use them to simplify and compare fractions.
The HCF for 4 and 20 is 4
The highest common factor (HCF) is the largest factor that two or more numbers have in common.
Factors and Multiples
HCF are important because we can use them to simplify and compare fractions.
The HCF for 4 and 20 is 4
The highest common factor (HCF) is the largest factor that two or more numbers have in common.
Factors and Multiples
HCF are important because we can use them to simplify and compare fractions.
HCF can also help you dividing other things into equal parts.
Factors and Multiples
HCF are important because we can use them to simplify and compare fractions.
HCF can also help you dividing other things into equal parts.
Let’s say you have 48 crayons and 60 coloured pencils. You want to put them into identical art kits for friends. You want each friend to get the same number of crayons and the same number of coloured pencils, with nothing left over.
"
Factors and Multiples
Let’s say you have 48 crayons and 60 coloured pencils. You want to put them into identical art kits for friends. You want each friend to get the same number of crayons and the same number of coloured pencils, with nothing left over.
"
1. Find the HCF: The HCF of 48 and 60 is 12.
2. Divide by the HCF:
- Crayons: 48 ÷ 12 = 4 crayons per kit
- Colored Pencils: 60 ÷ 12 = 5 colored pencils per kit
3. Create Your Kits: Since the HCF is 12, you can make 12 complete art kits. Each kit will have 4 crayons and 5 colored pencils, and you’ll use up all the crayons and pencils perfectly.
You can often use your times table knowledge to quickly identify common factors.
We can immediately see that 6 is the highest factor shared by both numbers. But with larger numbers this may not be quite as easy. Let's look at something more complicated.
What is the Highest Common Factor of these numbers?
What is the Highest Common Factor of these numbers?
First let's write each number as a product of its prime factors.
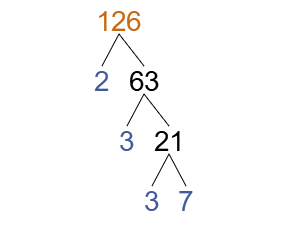
What is the Highest Common Factor of these numbers?
First let's write each number as a product of its prime factors.

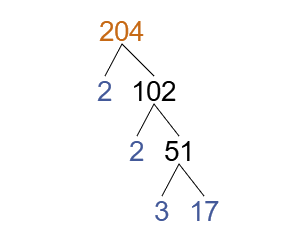
We can see that they both share 2 and 3 as common factors.
What is the Highest Common Factor of these numbers?
First let's write each number as a product of its prime factors.


Factors and Multiples
A multiple of a number is the result of multiplying it by another whole number.
Example: Some multiples of 5 are 5, 10, 15, 20, 25, 30, ...
Notice that multiples are what you see in a number's times table!
Factors and Multiples
HCF and LCM
The lowest common multiple (LCM) is the smallest multiple that two or more numbers share.
Example: Find the LCM of 4 and 6.
Multiples of 4: 4, 8, 12, 16, 20, 24, ...
Multiples of 6: 6, 12, 18, 24, 30, ...
The common multiples are 12, 24, ...
The lowest common multiple is 12.
HCF and LCM
There are two strategies we can use to find LCM:
1. Find LCM by Listing Multiples.
As you've already seen, we can find LCM by listing the multiples of each number until we find the first common multiple.
The lowest common multiple of 7 and 9 is 63
HCF and LCM
1. Find LCM by Listing Multiples.
The lowest common multiple of 7 and 9 is 63
2. Find LCM by by Prime Factorization.
You can also find LCM by listing all the prime factors of the numbers.
Now pick each number as it appears the most.
HCF and LCM
1. Find LCM by Listing Multiples.
The lowest common multiple of 7 and 9 is 63
2. Find LCM by by Prime Factorization.
You can also find LCM by listing all the prime factors of the numbers.
Now pick each number as it appears the most.
The longest entry for 3 is [3 x 3 x 3]
The longest entry for 2 is [2 x 2]
HCF and LCM
1. Find LCM by Listing Multiples.
The lowest common multiple of 7 and 9 is 63
2. Find LCM by by Prime Factorization.
Now pick each number as it appears the most.
The longest entry for 3 is [3 x 3 x 3]
The longest entry for 2 is [2 x 2]
The lowest common multiple of 27 and 36 is 108
HCF and LCM
LCM are important because we can use them to compare, add and subtract fractions.
HCF and LCM
LCM are important because we can use them to compare, add and subtract fractions.
HCF and LCM
LCM are important because we can use them to compare, add and subtract fractions.
The LCM for 9 and 4 is 36, so we multiply 9 x 4 = 36
The LCM for 9 and 4 is 36, so we multiply 12 x 3 = 36
HCF and LCM
LCM are important because we can use them to compare, add and subtract fractions.
HCF and LCM
LCM are important because we can use them to compare, add and subtract fractions.
Now that both fractions have the same denominator, we can add the numerators.
You can learn more about this in our tutorial dedicated to fractions. For now it's just important to remember that finding the LCM is essential for these types of calculations.
HCF and LCM
LCM are important because we can use them to compare, add and subtract fractions.
LCM are also useful for word problems and real-life situations.
Let's say you're looking at two routes:
"
Bus A & B both arrives at 10am. After that, Bus A arrives every 15 minutes and Bus B arrives every 22 minutes.
Anna arrives on Bus A and John arrives on bus B. They missed the 10am busses. What is the earlies they can meet up if they both want to arrive at exactly the same time?
"
Bus A & B both arrives at 10am. After that, Bus A arrives every 15 minutes and Bus B arrives every 22 minutes.
Anna arrives on Bus A and John arrives on bus B. They missed the 10am busses. What is the earlies they can meet up if they both want to arrive at exactly the same time?
If we want, we can work out the arrival times of each bus:
As you can see, this is not very efficient as we may have to keep going for a very long time before we find an overlapping time.
"
Bus A & B both arrives at 10am. After that, Bus A arrives every 15 minutes and Bus B arrives every 22 minutes.
Anna arrives on Bus A and John arrives on bus B. They missed the 10am busses. What is the earlies they can meet up if they both want to arrive at exactly the same time?
Instead we can look for the lowest common multiple of 15 and 22:
So, the two bus routes will align every 330 minutes. Thus the time will be
"
Bus A & B both arrives at 10am. After that, Bus A arrives every 15 minutes and Bus B arrives every 22 minutes.
Anna arrives on Bus A and John arrives on bus B. They missed the 10am busses. What is the earlies they can meet up if they both want to arrive at exactly the same time?
Instead we can look for the lowest common multiple of 15 and 22:
So, the two bus routes will align every 330 minutes. Thus the time will be
Prime Numbers
What are prime numbers?
A prime number is a number that only has 2 factors. This means that is cannot be divided evenly by any other number.
Examples:
Prime numbers: 2, 3, 5, 7, 11, 13, 17, 19...
Non-prime numbers: Non-prime numbers: 4, 6, 8, 9, 10...
Interesting facts! The number 1 is not prime because it has only one factor. The number 2 is the only even prime number.
Prime Numbers
How to check if a number is prime:
- Start dividing the number by smaller numbers (starting from 2).
- If it can be divided evenly by any number other than 1 and itself, it’s not prime.
- If no division works, it’s prime!
Example: Is 7 prime?
Can only be divided by 1 and 7 → Prime!
Example: Is 9 prime?
Can be divided by 1, 3, and 9 → Not prime.
Prime Numbers
Practice questions:
Is 13 a prime number?
List all prime numbers between 1 and 20.
Which of these is not prime?
A) 7 B) 9 C) 11 D) 13
Yes, 13 is a prime number, the only numbers that can divide 13 evenly are 1 and 13 itself!
2, 3, 5, 7, 11, 13, 17, 19
9 is not a prime number - it is divisible by 3.
Square Numbers
A square number is the result of multiplying a number by itself.
Example: 4 x 4 = 16, so 16 is a square number.
Common square numbers:
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25, and so on!
So, 1, 4, 9, 16, 25, ... are all square numbers.
Square Numbers
A square number is the result of multiplying a number by itself.
Square numbers can be visualised as a two dimensional square.
Cube Numbers
A cube number is the result of multiplying a number by itself a total of three times.
Example: 3 x 3 x 3 = 27, so 27 is a cube number.
Common cube numbers:
1³ = 1
2³ = 8
3³ = 27
4³ = 64, and so on!
So, 1, 8, 27, 64, 125 ... are all cube numbers.
Cube Numbers
A cube number is the result of multiplying a number by itself a total of three times.
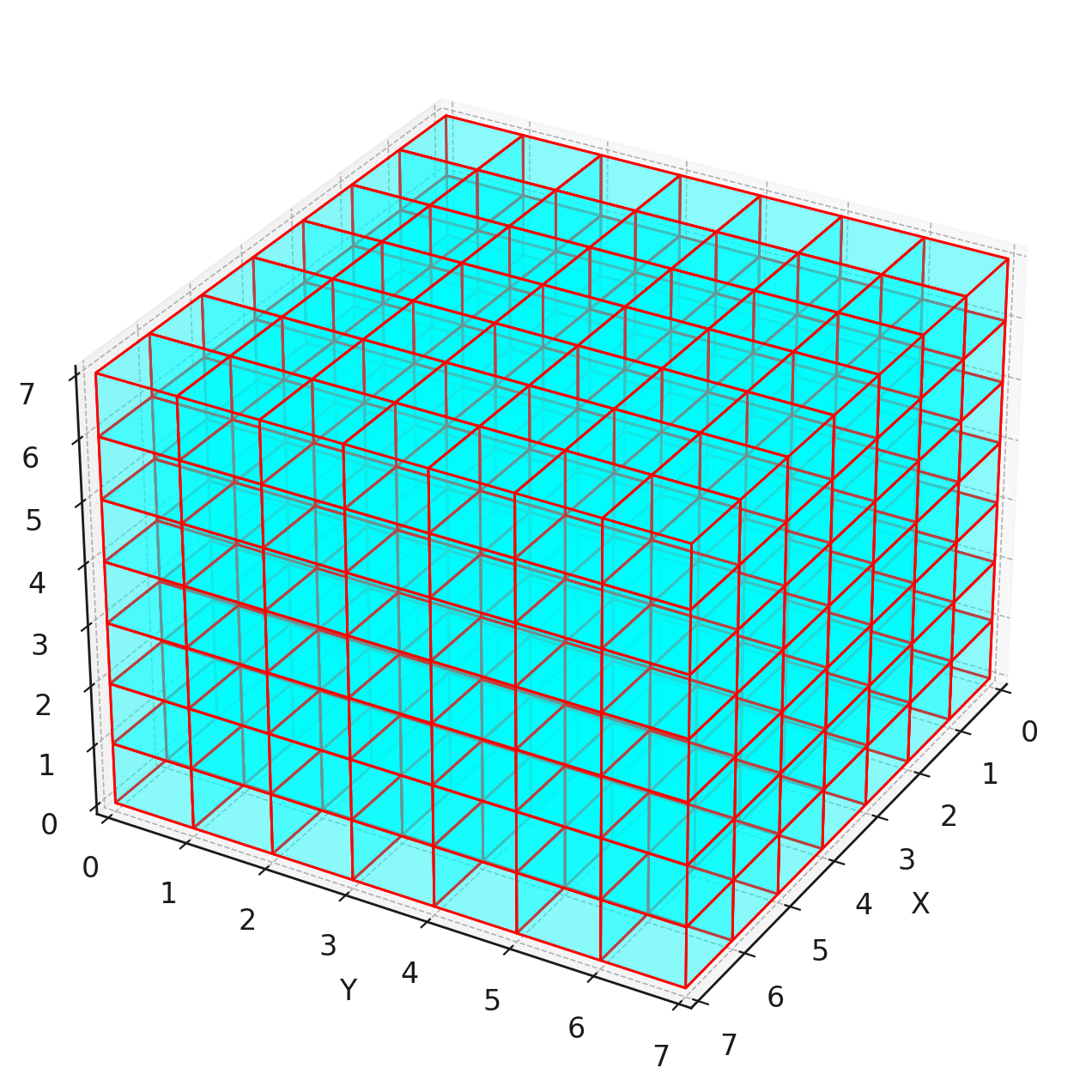
Cube numbers can be visualised as a three dimensional cube.
Square and Cube Numbers
Practice:
What is 7²?
What is 5³?
Is 36 a square number?
List all the square numbers between 1 and 50.
What is the cube of 3?
7 x 7 = 49
5 x 5 x 5 = 125 (5 x 5 = 25, then 25 x 5 = 125)
Is there a whole number that you can multiply by itself to get 36? Yes! 6 x 6 = 36. So 36 is a square number.
1,4,9,16,25,36,49
3 × 3 × 3= 27