11+ Maths
Measurements
Objective: Learn how to measure quantities, understand units, and convert between them accurately.
Why It Matters: Measurement helps us compare, calculate, and make decisions in everyday life, like measuring distance, time, or ingredients.
Key Ideas:
- Measurement determines “how much” of something there is.
- It is essential in daily life, science, and technology.
11+ Maths
Measurements
Types of Measurements
Length: Metres, centimetres, kilometres, miles, etc.
Mass: Kilograms, grams.
Volume: Litres, millilitres.
Time: Seconds, minutes, hours, days.
Temperature: Degrees Celsius.
Area: Square metres.
Length
Mass
Volume
Time
Temperature
Area
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Millimetres (mm) are very small measurements. You would use them to measure e.g. the thickness of a coin.
The prefix "milli" comes from Latin "mille" which means 1,000.
There are 1,000 millimetres in a metre.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Centimetres (cm) are small measurements used for everyday objects. You would use them to measure the length of a pencil or the width of a notebook.
The prefix "centi" comes from the Latin "centum", meaning 100. There are 100 centimetres in a metre.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Decimetres (dm) are medium-sized measurements, equal to 10 centimetres or one-tenth of a metre.
Decimetres are not commonly used in everyday life but can appear in scientific contexts or for educational purposes. The prefix "deci" comes from the Latin "decimus", meaning tenth.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Metres (m) are the standard unit of length in the metric system, used to measure medium to large distances. You would use metres to measure, for example, the height of a door, the length of a room, or the width of a garden.
The word "metre" comes from the Greek "metron", meaning measure.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Kilometres (km) are used to measure long distances, such as the length of roads or journeys. For example, the distance from one city to another might be measured in kilometres.
The prefix "kilo" comes from the Greek "chilioi", meaning 1,000. There are 1,000 metres in a kilometre.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Fun fact:
Generally Latin prefixes (milli-, centi- and deci-) are used for divisions, while Greek prefixes are used for multiples (hecto-, deca-, kilo-, mega-, giga-).
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
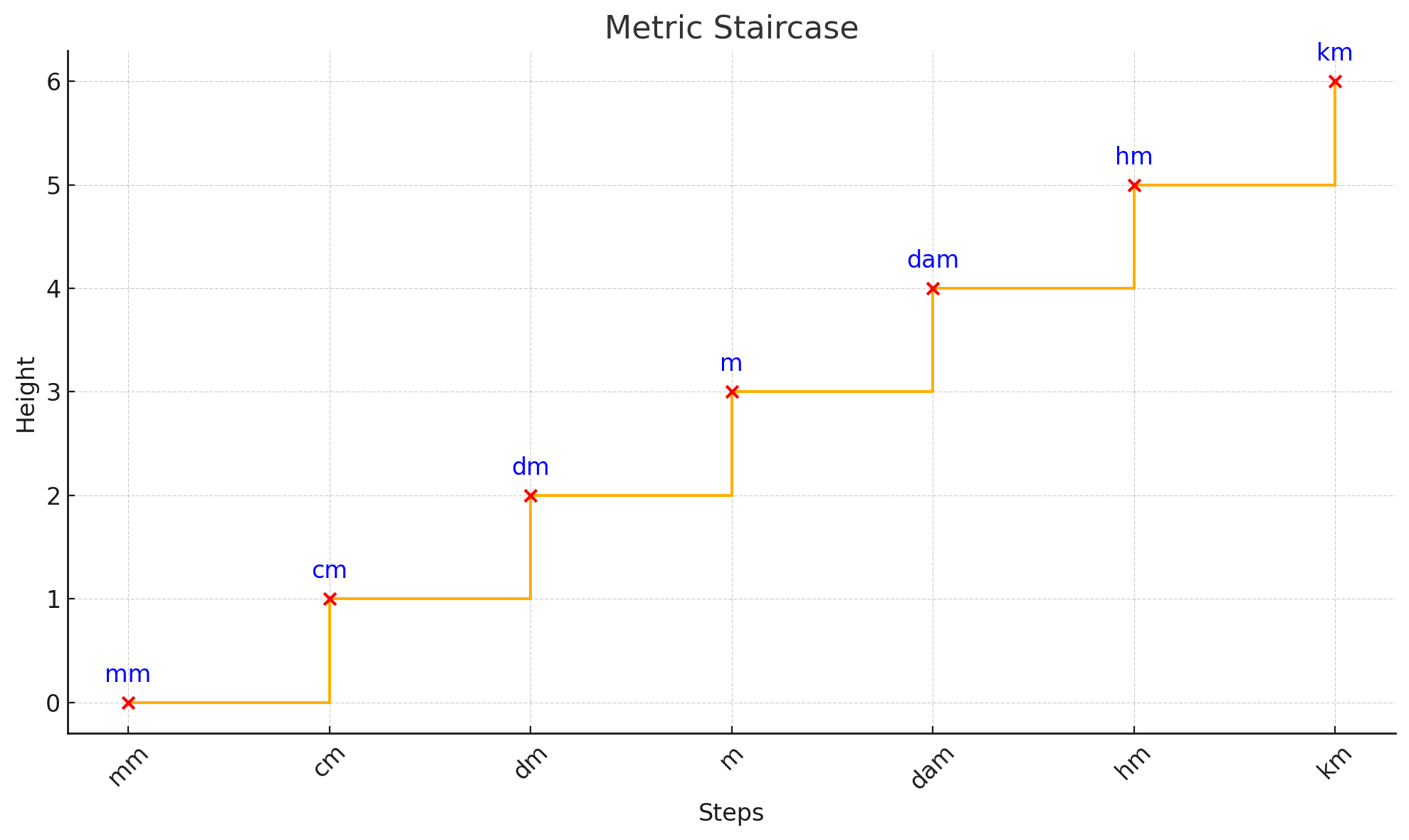
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Imagine that we start with 1,000 mm.
1000 mm
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
If we want to change that into cm, we simply divide by 10:
1,000 / 10 = 100
1000 mm
cm
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
To go from cm to dm, we can just repeat the process of dividing by 10:
100 / 10 = 10
1000 mm
cm
dm
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Finally, from dm to m we can divide by ten again: 10 / 10 = 1
We can see that 1,000 mm turned out to
be 1 m
1000 mm
cm
dm
m
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
If we move the other way on the scale, we multiply instead of dividing.
Moving down the stairs, we x 10 for each step.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Let's say we have 0.5 m.
0.5 m
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Let's say we have 0.5 m.
To move to dm, we multiply by ten.
0.5 x 10 = 5 dm.
5 dm
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Let's say we have 0.5 m.
Again, we multiply by 10 to move from dm to cm:
5 x 10 = 50 cm.
50 cm
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Let's say we have 0.5 m.
And finally, we multiply by 10 again to go from cm to mm:
50 x 10 = 500 mm.
500 mm
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Here is a more complicated example
What is 20m in mm?
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Here is a more complicated example
What is 20m in mm?
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Here is a more complicated example
What is 20m in mm?
\times 10
\times 10
\times 10
20
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Here is a more complicated example
What is 20m in mm?
\times 10
\times 10
\times 10
200
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Here is a more complicated example
What is 20m in mm?
\times 10
\times 10
\times 10
2000
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Here is a more complicated example
What is 20m in mm?
\times 10
\times 10
\times 10
20000
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
The metric system is based on a very simple principle of dividing or multiplying by 10 as we change units up or down. You can think of it like a staircase:
Here is a more complicated example
20m are mm
\times 10
\times 10
\times 10
20000
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Metric
This regularity within the metric system makes it easy to remember and to convert quickly from one unit of measurement to another.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Unlike the metric system, the imperial system does not follow a decimal principle or even a fixed system of conversion.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Inches (in) is a small measurement about the length of a standard paperclip.
The word comes from Latin "uncia".
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
Feet (ft ) is used to measure things of a medium length. As the name implies, it's about the length of man's foot.
There are 12 inches in 1 foot
\div 12
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
A yard (yd) is slightly shorter than a metre and you'd use it to measure longer lengths, such as the length of a football pitch.
There are 3 feet in a yard.
\div 3
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Length measures distance: how long or tall something is.
In the UK we use both metric and imperial measurements.
Metric
Millimetres (mm)
Centimetres (cm)
Decimetre (dm)
Metres (m)
Kilometres (km)
Imperial
Inches (in)
Feet (ft)
Yards (yd)
Miles (mi)
A mile (mi) is used to measure longer distances, such distances between cities.
There are 1760 yards in a mile.
\div 1760
Mass
Length
Mass
Volume
Time
Temperature
Area
Mass
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
Mass
Mass
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
To a scientist, mass and weight is not the same: Mass is the amount of stuff in an object and would be the same whether you're on Earth or on the Moon - even though the Moon has a lower gravity.
Weight is how heavy something feels because of gravity. Gravity pulls objects down, and this force makes up their weight.
Mass
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
To a scientist, mass and weight is not the same: Mass is the amount of stuff in an object and would be the same whether you're on Earth or on the Moon - even though the Moon has a lower gravity.
Weight is how heavy something feels because of gravity. Gravity pulls objects down, and this force makes up their weight.
Don't worry if you feel you don't fully understand the difference between mass and weight. For your 11+ you can think of them interchangeably.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
To a scientist, mass and weight is not the same: Mass is the amount of stuff in an object and would be the same whether you're on Earth or on the Moon - even though the Moon has a lower gravity.
Weight is how heavy something feels because of gravity. Gravity pulls objects down, and this force makes up their weight.
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
A kilogram (kg) is commonly used for heavier objects like a bag of rice or a watermelon.
A litre of water has the mass ("weight") of 1 kg.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
Hectograms (hg) and Decagrams (dg) are not very commonly used in the UK, but knowing that they exist is is important to understand the metric mass system.
In some countries they are more frequently used for everyday things.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
Gram (g) is the base unit of mass in the metric system, used for measuring small objects like a slice of cheese or a paperclip.
In the UK we often spell it "grammes".
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
The other units get their name from grams:
Kilo - 1,000
Hecto - 100
Deca - 10
As you can see the system is decimal just like the metric measurements of length.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
\div 10
\div 10
\div 10
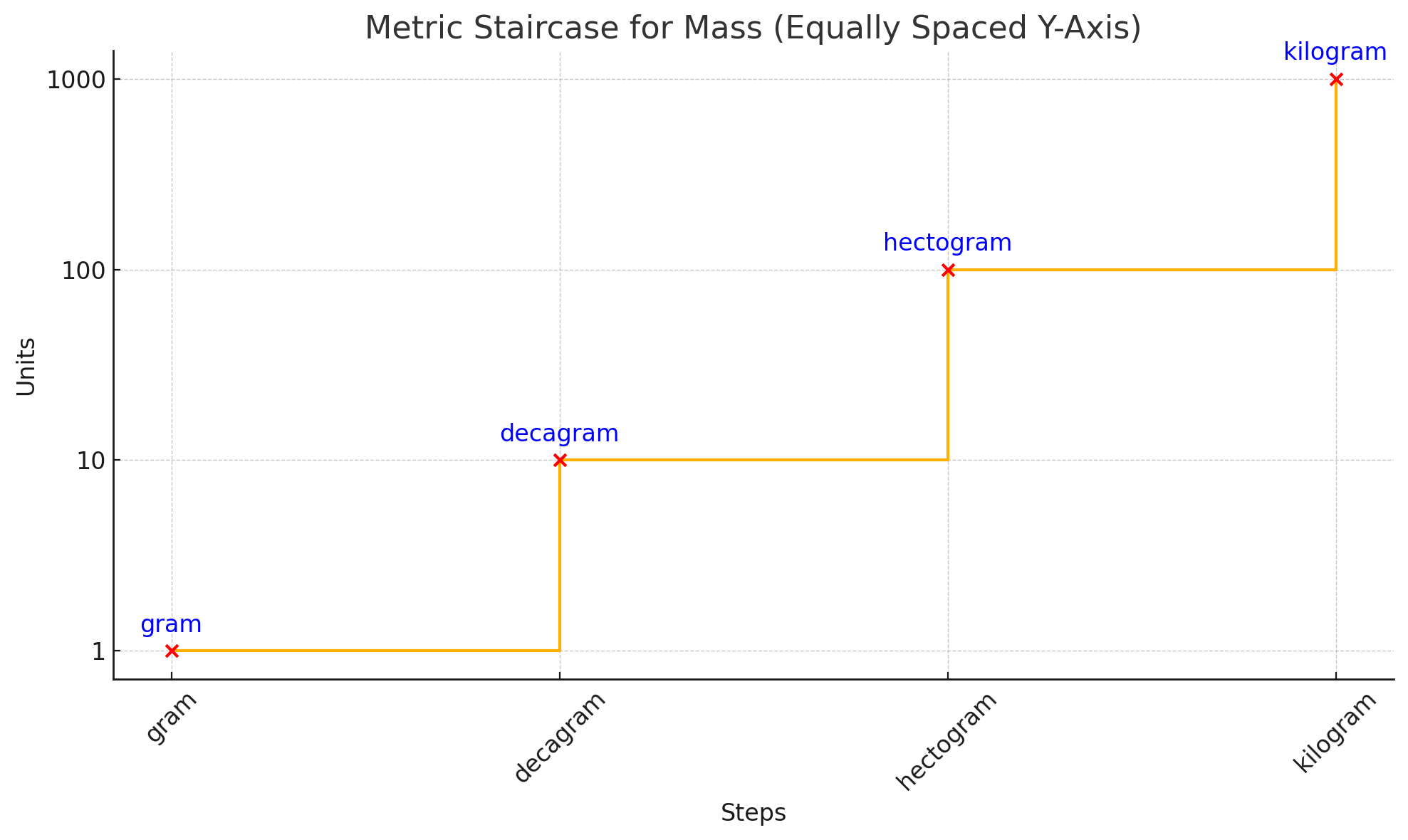
Going up the scale we divide by 10 each step.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Mass measures how much matter is in an object. It’s often referred to as “weight” in everyday language.
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
\times 10
\times 10
\times 10
Going down the scale we multiply by 10 each step.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Converting from 2000 grammes to kilogrammes:
2,000 g \div 10 = 200 dg\\
200 dg \div 10 = 20 hg\\
20 hg \div 10 = 2 kg
\div 10
\div 10
\div 10
2,000g = 2kg
2
20
200
2000
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Imperial
Ounces (oz)
Pounds (lb)
Stones (st)
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
As for the imperial length measurements, imperial mass units do not follow a fixed system with equal intervals between each unit.
There are 16 oz in 1 lb and there are 14 lb in 1 stone.
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Converting mass
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
For your 11+ you are unlikely to be asked to convert between metric and imperial. If you are asked, you will normally be provided with a rough figure to use for the conversion. You may be given a question similar to this:
16 ounces = 1 pound
2.2 pounds = 1 kg.
How many ounces are there in 5 kg?
"
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Converting mass
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
16 ounces = 1 pound
2.2 pounds = 1 kg.
How many ounces are there in 5 kg?
"
Working backwards from 5kg, we see that we need to multiply by 2.2 to get pounds, then multiply again by 16 to get ounces.
2.2
16
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Converting mass
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
16 ounces = 1 pound
2.2 pounds = 1 kg.
How many ounces are there in 5 kg?
"
x 2.2
x 16
5 \times 2.2 = 11\\
11 \times 16 = 176\\
\boxed{176 oz}
Types of Measurements
Length
Mass
Volume
Time
Temperature
Area
Converting mass
Just as for length, in the UK we use both metric and imperial
measurements for mass.
Metric
Kilogram (kg)
Hectogram (hg)
Decagram (dg)
Gram (g)
You will be expected to know how to convert within the metric scale from memory. Remember:
1 kg = 1,000 g
Volume
Length
Mass
Volume
Time
Temperature
Area
Volume
Length
Mass
Volume
Time
Temperature
Area
Volume
Types of Measurements
Volume measures how much space an object takes up. It’s used to measure liquids, gases, or the size of 3D objects like boxes or bottles.
Length
Mass
Volume
Time
Temperature
Area
Volume
Types of Measurements
Volume measures how much space an object takes up. It’s used to measure liquids, gases, or the size of 3D objects like boxes or bottles.
The metric system measures volume using litres (L) as the base unit. A litre is commonly used to measure liquids like water or juice.
litres (L)
Length
Mass
Volume
Time
Temperature
Area
Volume
Volume measures how much space an object takes up. It’s used to measure liquids, gases, or the size of 3D objects like boxes or bottles.
The metric system measures volume using litres (l) as the base unit. A litre is commonly used to measure liquids like water or juice.
litres (l)
decilitre (dl)
centilitre (cl)
millilitre (ml)
\div 10
\div 10
\div 10
As with the other metric units, you divide or multiply by 10 when moving up or down the scale.
Length
Mass
Volume
Time
Temperature
Area
Volume
Volume measures how much space an object takes up. It’s used to measure liquids, gases, or the size of 3D objects like boxes or bottles.
The metric system measures volume using litres (l) as the base unit. A litre is commonly used to measure liquids like water or juice.
litres (l)
decilitre (dl)
centilitre (cl)
millilitre (ml)
\div 10
\div 10
\div 10
As with the other metric units, you divide or multiply by 10 when moving up or down the scale.
1,000 \text{ millilitres}
100 \text{ centilitres}
10 \text{ decilitres}
1 \text{ litre}
Length
Mass
Volume
Time
Temperature
Area
Volume
Volume measures how much space an object takes up. It’s used to measure liquids, gases, or the size of 3D objects like boxes or bottles.
The metric system measures volume using litres (l) as the base unit. A litre is commonly used to measure liquids like water or juice.
As with the other metric units, you divide or multiply by 10 when moving up or down the scale.
litres (l)
decilitre (dl)
centilitre (cl)
millilitre (ml)
\div 10
\div 10
\div 10
Try this yourself:
How much is 150ml in litres?
Length
Mass
Volume
Time
Temperature
Area
Volume
Volume measures how much space an object takes up. It’s used to measure liquids, gases, or the size of 3D objects like boxes or bottles.
The metric system measures volume using litres (l) as the base unit. A litre is commonly used to measure liquids like water or juice.
As with the other metric units, you divide or multiply by 10 when moving up or down the scale.
litres (l)
decilitre (dl)
centilitre (cl)
millilitre (ml)
\div 10
\div 10
\div 10
Try this yourself:
How much is 150ml in litres?
150 \text{ml} \div 10 = 15 \text{cl}\\
15\text{cl} \div 10 = 1.5 \text{dl}\\
1.5 \text{dl} = \boxed{0.15 \text{l}}
Length
Mass
Volume
Time
Temperature
Area
Volume
Volume measures how much space an object takes up. It’s used to measure liquids, gases, or the size of 3D objects like boxes or bottles.
The metric system measures volume using litres (l) as the base unit. A litre is commonly used to measure liquids like water or juice.
As with the other metric units, you divide or multiply by 10 when moving up or down the scale.
litres (l)
decilitre (dl)
centilitre (cl)
millilitre (ml)
\div 10
\div 10
\div 10
Try this yourself:
How much is 150ml in litres?
150 \text{ml} \div 10 = 15 \text{cl}\\
15\text{cl} \ div 10 = 1.5 \text{dl}\\
1.5 \text{dl} = \boxed{0.15 \text{l}}
Imperial units
Volume too has some imperial units. The one you are most likely to come across in the UK is Pint (pt).
Pints are still used in the UK by many people to measure drinks like milk, beer, or juice.
| Length | Mass | Volume |
|---|---|---|
| metre |
kilogram | litre |
| decimetre |
hectogram | decilitre |
| centimetre |
decagram | centilitre |
| millimetre |
gram | millilitre |
Here is a summary of the metric units we have discussed:
Length
Mass
Volume
Time
Temperature
Area
Volume
Here is a summary of the metric units we have discussed:
You are more likely to come across the ones highlighted above.
| Length | Mass | Volume |
|---|---|---|
| metre |
kilogram | litre |
| decimetre |
hectogram | decilitre |
| centimetre |
decagram | centilitre |
| millimetre |
gram | millilitre |
Length
Mass
Volume
Time
Temperature
Area
Volume
Here is a summary of the metric units we have reviewed:
But learning the whole table will help you remember how to convert from one to another:
To move up, you divide by 10.
\div 10
| Length | Mass | Volume |
|---|---|---|
| metre |
kilogram | litre |
| decimetre |
hectogram | decilitre |
| centimetre |
decagram | centilitre |
| millimetre |
gram | millilitre |
Length
Mass
Volume
Time
Temperature
Area
Volume
Here is a summary of the metric units we have reviewed:
But learning the whole table will help you remember how to convert from one to another:
To move down, you multiply by 10.
\times10
| Length | Mass | Volume |
|---|---|---|
| metre |
kilogram | litre |
| decimetre |
hectogram | decilitre |
| centimetre |
decagram | centilitre |
| millimetre |
gram | millilitre |
Length
Mass
Volume
Time
Temperature
Area
Volume
Here is a summary of the metric units we have reviewed:
\times10
| Length | Mass | Volume |
|---|---|---|
| metre |
kilogram | litre |
| decimetre |
hectogram | decilitre |
| centimetre |
decagram | centilitre |
| millimetre |
gram | millilitre |
The only common unit left out is kilometre (km).
It actually fits in the metric table too, but for now it's easier to just remember this:
kilometre (km)
Length
Mass
Volume
Time
Temperature
Area
Volume
Here is a summary of the metric units we have reviewed:
\times10
| Length | Mass | Volume |
|---|---|---|
| metre |
kilogram | litre |
| decimetre |
hectogram | decilitre |
| centimetre |
decagram | centilitre |
| millimetre |
gram | millilitre |
1
= 1,000 metres (m)
The only common unit left out is kilometre (km).
It actually fits in the metric table too, but for now it's easier to just remember this:
kilometre (km)
Length
Mass
Volume
Time
Temperature
Area
Volume
Time
\times10
Length
Mass
Time
Temperature
Area
Volume
Time
Length
Mass
Time
Temperature
Area
Volume
Time
The way we measure time is different from length, mass and volume. There is no decimal system. Instead time takes inspiration from the degrees of a circle.
Length
Mass
Time
Temperature
Area
Volume
Time
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
\begin{align*}
& 60 \text{ seconds } \rightarrow 1 \text{ minute (min)}\\
& 60 \text{ minutes } \rightarrow 1 \text{ hour (h)}\\
& 24 \text{ hours } \rightarrow 1 \text{ day}\\
& 7 \text{ days } \rightarrow 1 \text{ week}\\
& 52 \text{ weeks } \rightarrow 1 \text{ year}\\
\end{align*}
As you can see, the units of time are not organised in a decimal way
Length
Mass
Time
Temperature
Area
Volume
Time
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
\begin{align*}
& 60 \text{ seconds } \rightarrow 1 \text{ minute (min)}\\
& 60 \text{ minutes } \rightarrow 1 \text{ hour (h)}\\
& 24 \text{ hours } \rightarrow 1 \text{ day}\\
& 7 \text{ days } \rightarrow 1 \text{ week}\\
& 52 \text{ weeks } \rightarrow 1 \text{ year}\\
\end{align*}
Just as you did for mass, volume and length, you can multiply and divide to move up and down the scale. But unlike the metric scale, time has different sized units, and therefore you must use different figures as you move up and down.
1\text{ week}
\times 7
7\text{ days}
\times 24
168\text{ hours}
\times 60
10,080\text{ min}
\times 60
604,800\text{ sec}
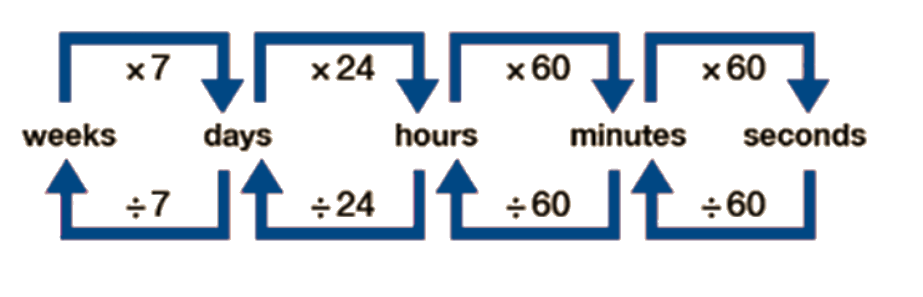
Length
Mass
Time
Temperature
Area
Volume
Time
Why don't we use a metric system for time?
In the olden days, before we had calculators, decimal units (units of 10) wasn't always the easiest to work with. While you can divide by 2 or 5, dividing by other numbers quickly become complicated:
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
?!
?!
Length
Mass
Time
Temperature
Area
Volume
Time
The number 60, however, can be divided by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30.
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
That made it a great number to use when people had to quickly calculate fractions of hours. It's the same reason we use
360 degrees in a circle.
Why don't we use a metric system for time?
Length
Mass
Time
Temperature
Area
Volume
Time
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
The circle of the clockface is split into 12 hours.
Length
Mass
Time
Temperature
Area
Volume
Time
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
The circle of the clockface is split into 12 hours.
Each of these sections also represent 5 minutes.
5 minutes
Length
Mass
Time
Temperature
Area
Volume
Time
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
The circle of the clockface is split into 12 hours.
Each of these sections also represent 5 minutes.
5 minutes
It is also because
30^\circ
360^\circ \div 12 = 30^\circ
1 hour
Length
Mass
Time
Temperature
Area
Volume
Time
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
The circle of the clockface is split into 12 hours.
Each of these sections also represent 5 minutes.
5 minutes
It is also because
30^\circ
360^\circ \div 12 = 30^\circ
1 hour
The hour hand goes round the clockface twice in 24 hours (a day). Each round is to form a full circle.
360^\circ
Length
Mass
Time
Temperature
Area
Volume
Time
10 \div 3 = 3 \frac{1}{3} \div 3 = 1 \frac{1}{9}
10 \div 4 = 2 \frac{1}{2} \div 4 = \frac{5}{8}
The circle of the clockface is split into 12 hours.
Each of these sections also represent 5 minutes.
5 minutes
It is also because
30^\circ
360^\circ \div 12 = 30^\circ
1 hour
The hour hand goes round the clockface twice in 24 hours (a day). Each round is to form a full circle.
360^\circ
A quarter of an hour is 15 minutes. During that time, the minute hand moves .
90^\circ
Length
Mass
Time
Temperature
Area
Volume
Time
For your 11+ you may be asked to calculate degrees on a clockface. This is an example of the type of questions you might expect:
What is the angle formed between the hour hand and the minute hand at 2PM?
"
Length
Mass
Time
Temperature
Area
Volume
Time
What is the angle formed between the hour hand and the minute hand at 2PM?
"
As you may recall, each hour on a clockface represents , because
30^\circ
360^\circ \div 12 = 30^\circ
Length
Mass
Time
Temperature
Area
Volume
Time
What is the angle formed between the hour hand and the minute hand at 2PM?
"
As you may recall, each hour on a clockface represents , because
30^\circ
360^\circ \div 12 = 30^\circ
Therefore, the difference between the hour hand being at 2 o'clock and the minute hand being at 12 o'clock, must be
360^\circ \div 12 = 30^\circ\\
30^\circ \times 2 = \boxed{60^\circ}
Temperature
Length
Mass
Time
Temperature
Area
Volume
Temperature
Length
Mass
Time
Temperature
Area
Volume
Temperature
Temperature measures how hot or cold something is, helping us understand weather, cooking, and scientific changes, using units like Celsius (°C) or Fahrenheit (°F).
Length
Mass
Time
Temperature
Area
Volume
Temperature
Temperature measures how hot or cold something is, helping us understand weather, cooking, and scientific changes, using units like Celsius (°C) or Fahrenheit (°F).
The meaning of zero
When we talked about length, mass, volume or time, zero meant literally nothing. A line with a length of 0 has no length at all.
When we measure temperature, a zero works a bit differently.
Length
Mass
Time
Temperature
Area
Volume
Temperature
The meaning of zero
We measure temperatures in many different scales, but the most commonly used in the UK is Celsius.
On the Celsius scale, 0°C is the point where water freezes to ice. It doesn't mean that there is no temperature. 0°C is simply a point on the scale. You need at least two points to make a scale, and the temperature at which water freezes was set to 0°C and the temperature water boils was set to 100°C.
Mathematically 0 works in the way you are used to. 0°C + 2°C = 2°C. But 0°C doesn't mean that there is no heat or cold.
Length
Mass
Time
Temperature
Area
Volume
Temperature
\Leftarrow \text{Colder}
\text{Warmer} \Rightarrow
Let's say that the temperature is -4°.
-4°.
Length
Mass
Time
Temperature
Area
Volume
Temperature
\Leftarrow \text{Colder}
\text{Warmer} \Rightarrow
Let's say that the temperature is -4°. Two hours later, the temperature has increased by 6°. In maths, we would write an increase of 6 as +6.
-4°.
Length
Mass
Time
Temperature
Area
Volume
Temperature
\Leftarrow \text{Colder}
\text{Warmer} \Rightarrow
Let's say that the temperature is -4°. Two hours later, the temperature has increased by 6°. In maths, we would write an increase of 6 as +6.
-4 + 6 = 2
\phantom{2}+1 +2 +3 +4 +5 +6
Length
Mass
Time
Temperature
Area
Volume
Temperature
\Leftarrow \text{Colder}
\text{Warmer} \Rightarrow
If the temperature now drops 4 degrees, we'd write
that as - 4° and simply subtract in the normal way.
2 -4 = -2
\phantom{2}-4 -3 -2 -1
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
While both Celsius (°C) and Fahrenheit (°F) measures temperature, the two scales were created with different reference points.
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100
°C
While both Celsius (°C) and Fahrenheit (°F) measures temperature, the two scales were created with different reference points.
On the Celsius scale, the temperature at which water freezes is defined as 0°C.
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100
°C
While both Celsius (°C) and Fahrenheit (°F) measures temperature, the two scales were created with different reference points.
On the Celsius scale, the temperature at which water freezes is defined as 0°C. The temperature at which water boils is defined as 100°C.
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
While both Celsius (°C) and Fahrenheit (°F) measures temperature, the two scales were created with different reference points.
On the Celsius scale, the temperature at which water freezes is defined as 0°C. The temperature at which water boils is defined as 100°C.
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100
°C
On the Fahrenheit scale, the same temperatures are 32°F and 212°F.
32 50 68 86 104 122 140 158 176 194 212
°F
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
While both Celsius (°C) and Fahrenheit (°F) measures temperature, the two scales were created with different reference points.
On the Celsius scale, the temperature at which water freezes is defined as 0°C. The temperature at which water boils is defined as 100°C.
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100
°C
On the Fahrenheit scale, the same temperatures are 32°F and 212°F.
32 50 68 86 104 122 140 158 176 194 212
°F
Note that the difference between the two points on the Celsius scale is exactly 100, while on the Fahrenheit scale it is 180. Therefore 1°F is smaller than 1°C.
100 - 0 = 100 degrees.
212 - 32 = 180 degrees.
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100
°C
32 50 68 86 104 122 140 158 176 194 212
°F
100 - 0 = 100 degrees.
212 - 32 = 180 degrees.
The formula to convert between Celsius and Fahrenheit is
°C = (°F - 32) \times \frac{5}{9}
For your 11+ you will not normally be required to memorise this formula. You may be given the formula and asked to do the conversion or you may be given some reference temperatures and asked to estimate different values. Let's try some of these questions together.
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
The formula to convert between Celsius and Fahrenheit is
°C = (°F - 32) \times \frac{5}{9}
For your 11+ you will not normally be required to memorise this formula. You may be given the formula and asked to do the conversion or you may be given some reference temperatures and asked to estimate different values. Let's try some of these questions together.
The formula to convert degrees Celsius to Fahrenheit is as follows:
How much is 50°F in °C?
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100
°C
32 50 68 86 104 122 140 158 176 194 212
°F
100 - 0 = 100 degrees.
212 - 32 = 180 degrees.
"
Length
Mass
Time
Temperature
Area
Volume
Temperature
Converting temperature
The formula to convert between Celsius and Fahrenheit is
°C = (°F - 32) \times \frac{5}{9}
For your 11+ you will not normally be required to memorise this formula. You may be given the formula and asked to do the conversion or you may be given some reference temperatures and asked to estimate different values. Let's try some of these questions together.
The formula to convert degrees Celsius to Fahrenheit is as follows:
How much is 50°F in °C?
°C = (°F - 32) \times \frac{5}{9}\Rightarrow
°C = (50 - 32) \times \frac{5}{9}\\
Let's start by filling in the value 50 from the question:
"
Length
Mass
Time
Temperature
Area
Volume
Converting temperature
The formula to convert between Celsius and Fahrenheit is
°C = (°F - 32) \times \frac{5}{9}
For your 11+ you will not normally be required to memorise this formula. You may be given the formula and asked to do the conversion or you may be given some reference temperatures and asked to estimate different values. Let's try some of these questions together.
The formula to convert degrees Celsius to Fahrenheit is as follows:
How much is 50°F in °C?
°C = (°F - 32) \times \frac{5}{9}\Rightarrow
°C = (50 - 32) \times \frac{5}{9}\\
Let's start by filling in the value 50 from the question:
°C = 18 \times \frac{5}{9}\Rightarrow °C = \frac{18 \times5}{1 \times 9}\\
°C = \frac{90}{9}\\
\boxed{°C = 10}
Now let's solve step-by-step for C:
"
Length
Mass
Time
Temperature
Area
Volume
Converting temperature
The formula to convert between Celsius and Fahrenheit is
For your 11+ you will not normally be required to memorise this formula. You may be given the formula and asked to do the conversion or you may be given some reference temperatures and asked to estimate different values. Let's try some of these questions together.
If 100°C = 212°F and 0°C = 32°F, how much is
122°F in °C?
"
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100
°C
32 50 68 86 104 122 140 158 176 194 212
°F
100 - 0 = 100 degrees.
212 - 32 = 180 degrees.
Length
Mass
Time
Area
Volume
Converting temperature
The formula to convert between Celsius and Fahrenheit is
For your 11+ you will not normally be required to memorise this formula. You may be given the formula and asked to do the conversion or you may be given some reference temperatures and asked to estimate different values. Let's try some of these questions together.
If 100°C = 212°F and 0°C = 32°F, how much is
122°F in °C?
"
As we mentioned we can see that the difference between the two is 100°C and 180°F. Since 50°C is half way between the two points, then the matching °F will be half way between 32 and 212:
212-32=180 \Rightarrow 180 \div 2 = 90\\
90+32 = \boxed{112}
Area
Temperature
Length
Mass
Time
Area
Volume
The formula to convert between Celsius and Fahrenheit is
For your 11+ you will not normally be required to memorise this formula. You may be given the formula and asked to do the conversion or you may be given some reference temperatures and asked to estimate different values. Let's try some of these questions together.
Area
Temperature
Length
Mass
Time
Area
Volume
Temperature
Area`
An area is the amount of space a 2D shape covers.
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
Such space will have a length and a width. The area is the product of these two peoperties:
\text{length} \times \text{width}
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
\text{length} \times \text{width}
You can imagine this as rows and columns. Let's say that we have 5 rows of 4:
4
5
5 \times 4 = 20
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
\text{length} \times \text{width}
You can imagine this as rows and columns. Let's say that we have 5 rows of 4:
4
5
5 \times 4 = 20
As you know your timetable, this is quite intuitive. 5 rows of 4, makes 20. For area it works in the same way.
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
\text{length} \times \text{width}
4
5
5 \times 4 = 20
As you know your timetable, this is quite intuitive. 5 rows of 4, makes 20. For area it works in the same way.
We could say that this area contains 20 "square cubes". We are then stating the total cubes contained within the area without saying anything about the length or width.
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
\text{length} \times \text{width}
4
5
5 \times 4 = 20
This is important, because 5 x 4 isn't the only way we can make arrange 20 cubes.
We could just as easily organise it as 4 x 5
5
4
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
\text{length} \times \text{width}
4
5
5 \times 4 = 20
This is important, because 5 x 4 isn't the only way we can make arrange 20 cubes.
We could just as easily organise it as 5 x 4, or 10 x 2.
4
5
10
2
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
\text{length} \times \text{width}
4
5
5 \times 4 = 20
4
5
10
2
This works the same way if we are counting cubes, cm, m or inches - or any other measurement of length.
cm
cm
m
m
in
in
Length
Mass
Time
Area
Volume
Temperature
Area
An area is the amount of space a 2D shape covers.
\text{length} \times \text{width}
4
5
5 \times 4 = 20
4
5
10
2
Because the area is a product of the two sides, we call the result "square". The product of two sides in cm is cm². The product of two sides measured in meter will be m² and in inches it will be in².
cm
cm
m
m
in
in
20cm²
20m²
20in²
Length
Mass
Time
Area
Volume
Temperature
Area
Some common units of area:
Square kilometres (km²)
Square metres (m²)
Square centimetres (cm²)
Square millimetres (mm²)
Metric
Square inch (in²)
Square foot (ft²)
Square yard (yd²)
Square mile (mi²)
Imperial
Length
Mass
Time
Area
Volume
Temperature
Area
Some common units of area:
Square kilometres (km²)
Square metres (m²)
Square centimetres (cm²)
Square millimetres (mm²)
Metric
Square inch (in²)
Square foot (ft²)
Square yard (yd²)
Square mile (mi²)
Imperial
Are (a) = 100 m²
Hectare (ha) = 100 ares
Acre (ac) = 4840 yd²
Length
Mass
Time
Area
Volume
Temperature
Area
Square kilometres (km²)
Square metres (m²)
Square centimetres (cm²)
Square millimetres (mm²)
Metric
Square inch (in²)
Square foot (ft²)
Square yard (yd²)
Square mile (mi²)
Imperial
Are (a) = 100 m²
Hectare (ha) = 100 ares
Acre (ac) = 4840 yd²
These are the ones you are most likely to come across for your 11+ assessment
Some common units of area:
Length
Mass
Time
Area
Volume
Temperature
Area
Square kilometres (km²)
Square metres (m²)
Square centimetres (cm²)
Square millimetres (mm²)
Metric
Square inch (in²)
Square foot (ft²)
Square yard (yd²)
Square mile (mi²)
Imperial
Are (a) = 100 m²
Hectare (ha) = 100 ares
Acre (ac) = 4840 yd²
These are the ones you are most likely to come across for your 11+ assessment
Some common units of area:
You will generally not be expected to convert from one to another without being provided the conversion rate
Converting between various units of area
While you are unlikely to be asked to convert from one unit of area to another, it's worth understanding the relationship between the length and width and the area that is the product.
Let us imagine this is Peter's farm:
Let us imagine this is Peter's farm:
10\text{m}
20\text{m}
His smallest field is 10m wide and 20m long. We would calculate the area as
10m \times 20m = 200m^2
20\text{m}
40\text{m}
Now imagine he wants to double both the length and the width.
The new area would be
His smallest field is 10m wide and 20m long. We would calculate the area as
10m \times 20m = 200m^2
20m \times 40m = 800m^2
If you compare the two areas and you may notice that we doubled each side, but the area increased 4 times.
800m^2
200m^2
20\text{m}
40\text{m}
If you compare the two areas and you may notice that we doubled each side, but the area increased 4 times.
800m^2
200m^2
This is because the area is the product of the two sides, so the increase of the area will be equal to: increase length x increase width
Thus, if you made each side 10 times longer, the area would increase by 100 times (10 x 10).
If you compare the two areas and you may notice that we doubled each side, but the area increased 4 times.
800m^2
200m^2
This is because the area is the product of the two sides, so the increase of the area will be equal to: increase length x increase width
Thus, if you made each side 10 times longer, the area would increase by 100 times (10 x 10).
This is important to remember if you are converting from e.g. cm to m:
1m \times 1m = 1m^2
100cm \times 100cm = 10,000cm^2
1m^2
10,000cm^2
Length
Mass
Time
Area
Volume
Temperature
Area
If you compare the two areas and you may notice that we doubled each side, but the area increased 4 times.
800m^2
200m^2
This is because the area is the product of the two sides, so the increase of the area will be equal to: increase length x increase width
Thus, if you made each side 10 times longer, the area would increase by 100 times (10 x 10).
This is important to remember if you are converting from e.g. cm to m:
1m \times 1m = 1m^2
100cm \times 100cm = 10,000cm^2
1m^2
10,000cm^2
=
Length
Mass
Time
Area
Volume
Temperature
Area
If you compare the two areas and you may notice that we doubled each side, but the area increased 4 times.
800m^2
200m^2
This is because the area is the product of the two sides, so the increase of the area will be equal to: increase length x increase width
Thus, if you made each side 10 times longer, the area would increase by 100 times (10 x 10).
This is important to remember if you are converting from e.g. cm to m:
1m \times 1m = 1m^2
100cm \times 100cm = 10,000cm^2
1m^2
10,000cm^2
=
Well done! You should now have a very good understanding of measurements: how to measure length, mass, volume, time, temperature and area and how to convert between different units of measurement.
With this information you should be one step closer to nailing the 11+ assessment. Good luck!
11+ Maths :: Measurements
By Pluspapers
