Fractions, decimals & Percentages

Understanding Fractions
A fraction represents a part of a whole and is written as two numbers separated by a line:
3
5
The numerator shows how many parts are considered
The denominator shows how many equal parts the whole is divided into
Understanding Fractions
A fraction represents a part of a whole and is written as two numbers separated by a line:
3
5
The numerator shows how many parts are considered
The denominator shows how many equal parts the whole is divided into

Understanding Fractions
A fraction represents a part of a whole and is written as two numbers separated by a line:
3
5
The numerator shows how many parts are considered
The denominator shows how many equal parts the whole is divided into

You can imagine this as simply 3 out of a total of 5
Understanding Fractions
Types of fractions:
- Proper fractions: Numerator is smaller than the denominator e.g
- Improper fractions: Numerator is greater than or equal to the denominator e.g
- Mixed numbers: A whole number combined with a fraction e.g
Understanding Fractions
Types of fractions:
- Proper fractions: Numerator is smaller than the denominator e.g
- Improper fractions: Numerator is greater than or equal to the denominator e.g
- Mixed numbers: A whole number combined with a fraction e.g
This is less than a whole
Understanding Fractions
Types of fractions:
- Proper fractions: Numerator is smaller than the denominator e.g
- Improper fractions: Numerator is greater than or equal to the denominator e.g
- Mixed numbers: A whole number combined with a fraction e.g
This is less than a whole
This is more than a whole
Understanding Fractions
Types of fractions:
- Proper fractions: Numerator is smaller than the denominator e.g
- Improper fractions: Numerator is greater than or equal to the denominator e.g
- Mixed numbers: A whole number combined with a fraction e.g
This is less than a whole
This is more than a whole
This is two whole and a bit
Simplifying fractions
To simplify a fraction, we need to first find the highest common factor (HCF).
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
What is the Highest Common Factor of these numbers?
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
What is the Highest Common Factor of these numbers?
First let's write each number as a product of its prime factors.
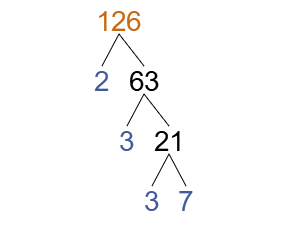
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
What is the Highest Common Factor of these numbers?
First let's write each number as a product of its prime factors.

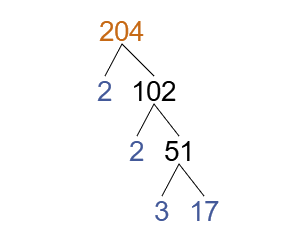
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
What is the Highest Common Factor of these numbers?
First let's write each number as a product of its prime factors.


We can see that they both share 2 and 3 as common factors.
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
What is the Highest Common Factor of these numbers?
First let's write each number as a product of its prime factors.


Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
Now that we know how to find the highest common factor of any number, let's return to the fractions.
Let's say we were to simplify . First we need to find out what the highest common factor is for 12 and 18.
Often we can do this through mental math. We know the factors of both 12 and 18 from our times tables:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
Divide both the numerator and denominator by the highest common factor (6):
÷ 6
÷ 6
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
You have successfully simplified the fraction.
÷ 6
÷ 6
Let's try a few more:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
You have successfully simplified the fraction.
÷ 6
÷ 6
Let's try a few more:
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
You have successfully simplified the fraction.
÷ 6
÷ 6
Let's try a few more:
÷ 4
÷ 4
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
You have successfully simplified the fraction.
÷ 6
÷ 6
Let's try a few more:
÷ 4
÷ 4
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
You have successfully simplified the fraction.
÷ 6
÷ 6
Let's try a few more:
÷ 4
÷ 4
÷ 2
÷ 2
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
You have successfully simplified the fraction.
÷ 6
÷ 6
Let's try a few more:
÷ 4
÷ 4
÷ 2
÷ 2
We can immediately see that 6 is the highest factor shared by both numbers. Sometimes it's not quite as easy. Let's look at something more complicated.
You have successfully simplified the fraction.
÷ 6
÷ 6
Let's try a few more:
÷ 4
÷ 4
÷ 2
÷ 2
÷ 5
÷ 5
Adding and Subtracting Fractions
When we add or subtract fractions with the same denominator, we add or subtract the numerators and keep the denominator the same.
For example,
Adding and Subtracting Fractions
When we add or subtract fractions with the same denominator, we add or subtract the numerators and keep the denominator the same.
For example,
Adding and Subtracting Fractions
When we add or subtract fractions with the same denominator, we add or subtract the numerators and keep the denominator the same.
For example,
Remember:
You can only add or subtract the numerator if the denominator is the same
Adding and Subtracting Fractions
When we add or subtract fractions with different denominators, we must first make the denominators the same. We do this by finding a common denominator for the fractions. Only then can we add or subtract the numerators.
2. Multiply each fraction by a number so that the denominators equal the LCM
3. Add/subtract the numerators
1. Find the lowest common multiple (LCM) of the denominators
Adding and Subtracting Fractions
1. Find the lowest common multiple (LCM) of the denominators
2. Multiply each fraction by a number so that the denominators equal the LCM
3. Add/subtract the numerators
Adding and Subtracting Fractions
1. Find the lowest common multiple (LCM) of the denominators
2. Multiply each fraction by a number so that the denominators equal the LCM
3. Add/subtract the numerators
12 is the lowest possible common multiple.
Adding and Subtracting Fractions
1. Find the lowest common multiple (LCM) of the denominators
2. Multiply each fraction by a number so that the denominators equal the LCM
3. Add/subtract the numerators
12 is the lowest possible common multiple.
Adding and Subtracting Fractions
1. Find the lowest common multiple (LCM) of the denominators
2. Multiply each fraction by a number so that the denominators equal the LCM
3. Add/subtract the numerators
12 is the lowest possible common multiple.
Multiplying Fractions
We multiply fractions by multiplying the numerators and denominators.
Example:
We can then simplify to
Multiplying Fractions
Let's do a few examples step-by-step:
Multiplying Fractions
Let's do a few examples step-by-step:
Multiplying Fractions
Let's do a few examples step-by-step:
Multiplying Fractions
Let's do a few examples step-by-step:
Simplify by dividing by the highest common factor:
Multiplying Fractions
Let's do a few examples step-by-step:
Simplify by dividing by the highest common factor:
Multiplying Fractions
Let's do a few examples step-by-step:
Multiplying Fractions
Let's do a few examples step-by-step:
Multiplying Fractions
Let's do a few examples step-by-step:
Multiplying Fractions
Let's do a few examples step-by-step:
Simplify by dividing by the highest common factor:
Dividing Fractions
We divide fractions by multiplying the first fraction by the reciprocal of the second fraction.
Example:
Dividing Fractions
We divide fractions by multiplying the first fraction by the reciprocal of the second fraction.
Example:
Keep the first fraction the same and flip the second
fraction
Dividing Fractions
We divide fractions by multiplying the first fraction by the reciprocal (flipped upside-down) of the second fraction.
Example:
Keep the first fraction the same and flip the second
fraction
Thus
Dividing Fractions
We divide fractions by multiplying the first fraction by the reciprocal of the second fraction.
Example:
Keep the first fraction the same and flip the second
fraction
Calculate so
You will have noticed that they way we multiply and divide fractions is quite similar. In both cases, you multiply the numerators and denominators, but for division you flip the second fraction around.
When you multiply: just keep and apply!
When you divide: keep, flip, and multiply!
"
Remember! For both multiply and divide, you multiply.
Just flip the second fraction first if you're dividing.
Dividing Fractions
We divide fractions by multiplying the first fraction by the reciprocal of the second fraction.
Example:
Keep the first fraction the same and flip the second
fraction
Calculate so
Understanding Decimals
A decimal is a number that represents a part of a whole using place value. The decimal point separates whole numbers and fractional parts.
For example, in 0.75:
- The 7 is in the tenths place
- The 5 is in the hundredths place
Understanding Decimals
Decimals and fractions are closely related
Let's look at an example:
Decimals and fractions are closely related
Let's look at an example:
This is the unit. It represent a whole number and not a decimal.
Decimals and fractions are closely related
Let's look at an example:
This is the "tenth" and represents tenths fraction of a unit. In this case the value is two, so it represents
Decimals and fractions are closely related
Let's look at an example:
This is the "hundredth" and represents hundredths fraction of a unit. In this case the value is four, so it represents
Decimals and fractions are closely related
Let's look at an example:
This is the "thousandth" and represents thousandths fraction of a unit. In this case the value is six, so it represents
Decimals and fractions are closely related
Let's look at an example:
We can write this number as
Converting Decimals to Fractions
As you will have noticed, it's easy to convert a decimal to a fraction. Simply write the number without the decimal point on top, this is the top of the fraction. For the denominator, write 1 followed by as many zeros as there are decimal places.
For example, for 0.5, write which we can simplify as
For 0.75, write
Remember to simplify fractions whenever possible.
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
Example: Round 0.763 to the nearest tenth.
0.763
tenth place
hundredths place is greater than 5
So we round up to 0.8.
To round a decimal to a given place:
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
Let's try one more, step-by-step
To round a decimal to a given place:
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
Round to nearest thousandth
To round a decimal to a given place:
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
First identify the thousandths place
To round a decimal to a given place:
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
First identify the thousandths place
Look at the number to the right of that place
To round a decimal to a given place:
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
First identify the thousandths place
Look at the number to the right of that place
In this case it is less than 5, so we simply cut off the number after the rounding place
To round a decimal to a given place:
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
First identify the thousandths place
Look at the number to the right of that place
In this case it is less than 5, so we simply cut off the number after the rounding place
To round a decimal to a given place:
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
To round a decimal to a given place:
One more example
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
To round a decimal to a given place:
Round to nearest tenth
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
To round a decimal to a given place:
First identify the tenth place
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
To round a decimal to a given place:
First identify the tenth place
Look at the number to the right of that place
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
To round a decimal to a given place:
First identify the tenth place
Look at the number to the right of that place
In this case it is more than 5, so we round up the tenth and cut off the rest of the numbers
Rounding Decimals
- Look at the digit to the right of the place value
- If the digit is 5 or greater, round up
- If the digit is less than 5, keep the place value the same
To round a decimal to a given place:
First identify the tenth place
Look at the number to the right of that place
In this case it is more than 5, so we round up the tenth and cut off the rest of the numbers
Understanding Percentages
Understanding Percentages
A percentage expresses a part of a whole as "out of 100". The symbol % is used. For example, 50% means "50 out of 100".
Percentages are commonly used to compare quantities, calculate discounts, and understand data in everyday life.
Understanding Percentages
A percentage expresses a part of a whole as "out of 100". The symbol % is used. For example, 50% means "50 out of 100".
Percentages are commonly used to compare quantities, calculate discounts, and understand data in everyday life.
Because a percentage is "something out of 100", they are identical to fractions with a denominator of 100:
Understanding Percentages
A percentage expresses a part of a whole as "out of 100". The symbol % is used. For example, 50% means "50 out of 100".
Percentages are commonly used to compare quantities, calculate discounts, and understand data in everyday life.
Because a percentage is "something out of 100", they are identical to fractions with a denominator of 100:
Understanding Percentages
A percentage expresses a part of a whole as "out of 100". The symbol % is used. For example, 50% means "50 out of 100".
Percentages are commonly used to compare quantities, calculate discounts, and understand data in everyday life.
Because a percentage is "something out of 100", they are identical to fractions with a denominator of 100:
Understanding Percentages
A percentage expresses a part of a whole as "out of 100". The symbol % is used. For example, 50% means "50 out of 100".
And since fractions can be expressed as decimals, so can percentages
Percentages are commonly used to compare quantities, calculate discounts, and understand data in everyday life.
Because a percentage is "something out of 100", they are identical to fractions with a denominator of 100:
Understanding Percentages
In this case, 10 hundredths is the same as 1 tenth:
And therefore 10% = 1/10 = 0.1
Understanding Percentages
Understanding Percentages
Understanding Percentages
Converting Decimals to Percentages
You can easily convert a decimal to a percentage by just multiplying the decimal by 100 and adding "%":
Example: Convert 0.6 to a percentage
0.6 = 6%
Example: Convert 0.43 to a percentage
0.43 = 43%
It's easy to understand when you remember that 0.43 is the same as
Converting Decimals to Percentages
You can easily convert a decimal to a percentage by just multiplying the decimal by 100 and adding "%":
Example: Convert 0.6 to a percentage
0.6 = 6%
Example: Convert 0.43 to a percentage
0.43 = 43%
It's easy to understand when you remember that 0.43 is the same as
Remember, 4 tenths is the same as 40 hundredths
You can reverse the operation if you want to go from a decimal to a percentage.
Simply divide the percentage by 100:
You can reverse the operation if you want to go from a decimal to a percentage.
Simply divide the percentage by 100:
This makes sense when you remember that a fraction is really just another way of saying "divided by" the denominator. As an example:
And therefore also
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
But not every fraction can be changed easily to a denominator of 100
As you will have seen converting fractions of 100 into percentages is easy, they are the same thing:
Converting Fractions to Percentages
Knowing this, you can convert any fraction to a percentage, if you can convert the denominator into 100.
Here we must use a different method to convert to percentage
Converting Fractions to Percentages
Do you remember how fractions are really just a division? If you divide the numerator by the denominator you will get a decimal number. And these decimal numbers can be converted into percentages.
Converting Fractions to Percentages
Do you remember how fractions are really just a division? If you divide the numerator by the denominator you will get a decimal number. And these decimal numbers can be converted into percentages.
Converting Fractions to Percentages
Do you remember how fractions are really just a division? If you divide the numerator by the denominator you will get a decimal number. And these decimal numbers can be converted into percentages.
Converting Fractions to Percentages
Do you remember how fractions are really just a division? If you divide the numerator by the denominator you will get a decimal number. And these decimal numbers can be converted into percentages.
Converting Fractions to Percentages
Do you remember how fractions are really just a division? If you divide the numerator by the denominator you will get a decimal number. And these decimal numbers can be converted into percentages.
A quick summary
How to convert fractions, percentages and decimals
Converting Between Fractions, Decimals and Percentages
Example: Complete the following table:
| Fraction | Decimal | Percentage |
|---|---|---|
| 25% | ||
| 0.4 |
1 ÷ 2 = 0.5
0.5
0.5 x 100 = 50
50%
0.25
25 ÷ 100
= 0.25
0.4 x 100 = 40
40%
Finding a Percentage of a Quantity
Often you will be asked to find a percentage of a number.
Find 25% of 50
There are several methods we can use to calculate this.
Lets look at them one by one.
Example:
1
Finding a Percentage of a Quantity
Find 25% of 50
Method
We know that 10% is . Often we can use this to quickly calculate other percentages. 25% is for example made up of 10% + 10% + 5% (half of 10%). In this example this gives us
1
Finding a Percentage of a Quantity
Find 25% of 50
Method
We know that 10% is . Often we can use this to quickly calculate other percentages. 25% is for example made up of 10% + 10% + 5% (half of 10%). In this example this gives us
Great for quick mental maths
1
2
Finding a Percentage of a Quantity
Find 25% of 50
Method
Because we can make any percentage into a decimal, we can use this to find the percentage of a number. Simply convert to decimal and multiply with the number:
Always works
Can be slower
2
3
Finding a Percentage of a Quantity
Find 25% of 50
Method
Another way to find the percentage of a number is to multiply by the percentage and dividing by 100. What you are basically doing is the same as in method 2, but in two steps.
3
3
Safe and easy
Can be slower
Percentage Increase & Decrease
Percentage Increase & Decrease
Percentage increase is when an original amount increases by a certain percentage.
If £100 increases by 10% you have £110:
Percentage Increase & Decrease
Percentage increase is when an original amount increases by a certain percentage.
If £100 increases by 10% you have £110:
You can think of the new amount as 100% + 10% = 110%. Therefore you can calculate it in one operation as 110% of £100:
Percentage Increase & Decrease
Percentage decrease is when an original amount decreases by a percentage of the original amount.
If £100 decreases by 10% you have £90:
Percentage Increase & Decrease
Percentage decrease is when an original amount decreases by a percentage of the original amount.
If £100 decreases by 10% you have £90:
You can think of the new amount as 100% - 10% = 90%. Therefore you can calculate it in one operation as 90% of £100:
Percentage Increase & Decrease
In summary, you can calculate percentage increase and decrease in two ways:
You can calculate the increase and add it to the original amount.
You can calculate the final percentage and calculate the amount from that.
Percentage Increase & Decrease
In summary, you can calculate percentage increase and decrease in two ways:
You can calculate the increase and add it to the original amount.
You can calculate the final percentage and calculate the amount from that.
Percentage Increase & Decrease
In summary, you can calculate percentage increase and decrease in two ways:
You can calculate the increase and add it to the original amount.
You can calculate the final percentage and calculate the amount from that.
Important!
All our calculations so far has been from the original amount. Sometimes you may be asked to calculate from the final amount. Let's have a look at the difference:
Important!
All our calculations so far has been from the original amount. Sometimes you may be asked to calculate from the final amount. Let's have a look at the difference:
Important!
All our calculations so far has been from the original amount. Sometimes you may be asked to calculate from the final amount. Let's have a look at the difference:
Original amount
20% Increase
Final amount
Important!
All our calculations so far has been from the original amount. Sometimes you may be asked to calculate from the final amount. Let's have a look at the difference:
Original amount
20% Increase
Final amount
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
Important!
Original amount
20% Increase
Final amount
In these cases you need to calculate from the original amount like you would solve an equation:
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
Important!
Original amount
20% Increase
Final amount
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
In these cases you need to calculate from the original amount like you would solve an equation:
We call the original amount x, as we are trying to solve for it
Important!
Original amount
20% Increase
Final amount
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
In these cases you need to calculate from the original amount like you would solve an equation:
We use 1.2 to represent 100% + 20% = 120% = 1.2 as a decimal
Important!
Original amount
20% Increase
Final amount
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
In these cases you need to calculate from the original amount like you would solve an equation:
We enter the final amount as we know this from the question.
Important!
Original amount
20% Increase
Final amount
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
In these cases you need to calculate from the original amount like you would solve an equation:
We move 1.2 to the other side to solve for x. We must reverse times to divide
Important!
Original amount
20% Increase
Final amount
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
In these cases you need to calculate from the original amount like you would solve an equation:
Finally we solve the equation: the original amount x equals 100 apples
Important!
Original amount
20% Increase
Final amount
If you are given only the final amount, you could not calculate the percentage directly of that, because 20% of 120 is not 20!
In these cases you need to calculate from the original amount like you would solve an equation:
Finding a Percentage Increase/Decrease
Imagine a pair of shoes cost £120 last week, and now they cost £90 and we wanted to work out what the percentage discount is.
We find this percentage decrease by calculating:
Change in value
Original number
x
100
Percentage change =
This formula works for finding both a percentage increase or a percentage decrease.
Finding a Percentage Increase/Decrease
Imagine a pair of shoes cost £120 last week, and now they cost £90 and we wanted to work out what the percentage discount is.
Change in value
Original number
x
100
Percentage change =
The change in value is £120 - £90 = £30
So, using the formula:
30
120
x
100
Percentage change =
= 25
So the percentage decrease is 25%.
Two odd types of sequences you may want to keep an eye out for is the Fibonacci sequence and prime number sequences.
Fibonacci sequence
prime number sequences
Since there is no simple system to prime numbers, we cannot easily express a prime number sequence as a function of n. The important thing is that you can identify these sequences as sequences of prime numbers.

Well done! You should now have a good understanding of fractions, decimals and percentages, how to convert between then and how you can use them to solve more complex questions.
With this information you should be one step closer to nailing the 11+ assessment. Good luck!